どんな記事
この記事を読むと以下のことが分かります。
- どんな勝率とリスクリワード比率なら勝てるのか(根拠)
- 損益分岐点をグラフで分かりやすく
- 損益分岐点をトレードで用いる際の "注意点"
追記
2019年2月7日 追記
「トータルプラス ≠ 破産しない」を追記。
トータルで勝つとは
トータルで勝つとはどういうことか、少し整理してみたいと思います。
- 勝率50%、リスクリワード比率(以下、RR比)が2倍の手法
- 1回のリスクを1万円として100回トレード
- 総利益は「50回 ✕ 2万円」で「100万円」
- 総損失は「50回 ✕ 1万円」で「50万円」
これが勝てる手法であることは、よく分かると思います。これを踏まえて考えると、以下が成り立ちそうです。
勝てる手法
少し計算式を変えると、リスクに対する1トレードあたりの期待値を算出することもできます。
試しに計算してみると、納得できると思います。
勝率50%、RR比1倍
勝率40%、RR比2倍
勝率50%でRR比が1倍、つまり、利益と損失が同じだとすると「期待値」はゼロ。利益も損失も発生しません。一方で、勝率が40%でRR比が2倍だと、0.2となり、「リスク1に対して、1トレードあたり0.2(20%)の利益が期待できる」という結果になります。
この記事でいうところの「損益分岐点」とは、「『期待値』がゼロになる『勝率とRR比の組み合わせ』」のことです。
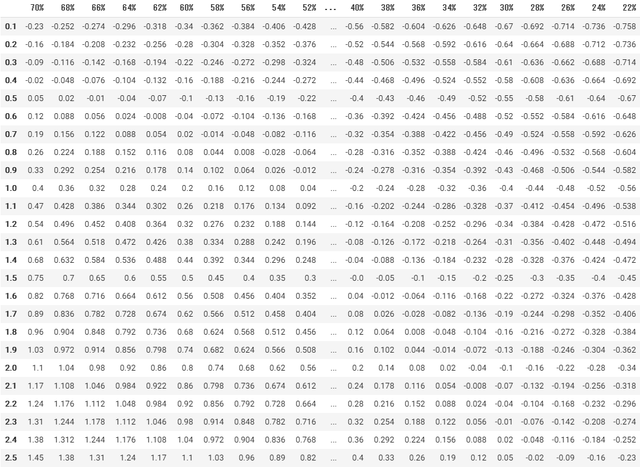
損益分岐点を計算してみる
最近よく使っている Pythonで「損益分岐点」をガッツリ算出してみました。(画像の下にPythonのコードも掲載しているので、興味がある方はご活用ください)
これだけだと、いまいち分かりづらいのでグラフを作成してみます。
import numpy as np
import pandas as pd
def calc_edge( win ,rr ) :
return win * rr - abs( 1 - win )
win_range = np.arange(0.7 ,0.2 ,-0.02)
rr_range = np.arange(0.1 ,4.1 ,0.1)
df_edge = pd.DataFrame()
for win in win_range :
for rr in rr_range :
edge = calc_edge( win ,rr )
df_edge.loc[rr ,f'{ win :.0%}'] = f'{ round( edge ,3 ) }'
df_edge分かりやすくグラフにしてみる
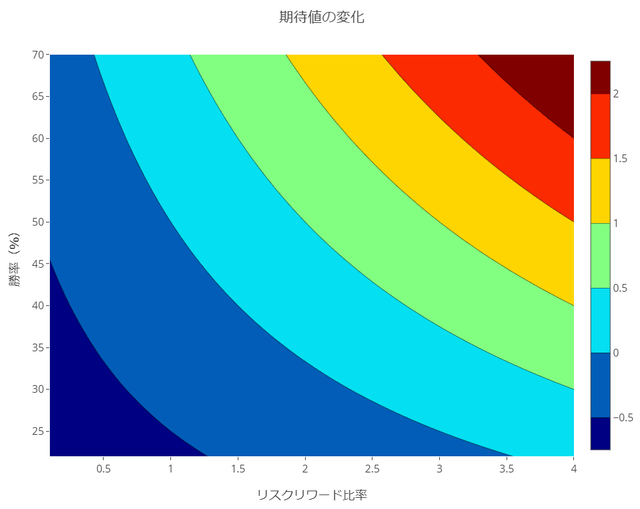
まずは、Contourグラフ(等高線)です。ゼロのラインよりも右上に位置していればプラスの期待値、左下だとマイナスの期待値です。つまり、ゼロのラインが「損益均衡点」を表しています。
投資をするときに目指すべきは、右上のエリアです。このエリアに入る「勝率」と「RR比」を目指せば、トータルでプラスになります。当然、ゼロのラインよりも右上に位置するほどに収益が大きくなります。
一時の〝まぐれ〟は、勝率やRR比で表すことができません。ルールを決めて、自分の勝率とRR比を把握・改善することで、トータルで勝てる10年選手になることができます。
次に、3DのSurfaceグラフを作成してみます。半透明のエリアよりも上がプラスの期待値で、下はマイナスの期待値です。半透明のエリアと交差しているところが「損益均衡点」ですね。(正直、Contourグラフの方が分かりやすいです)
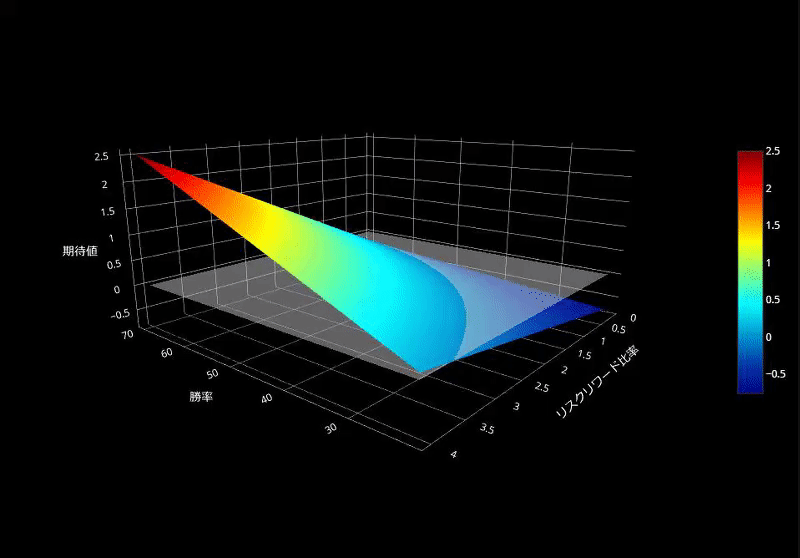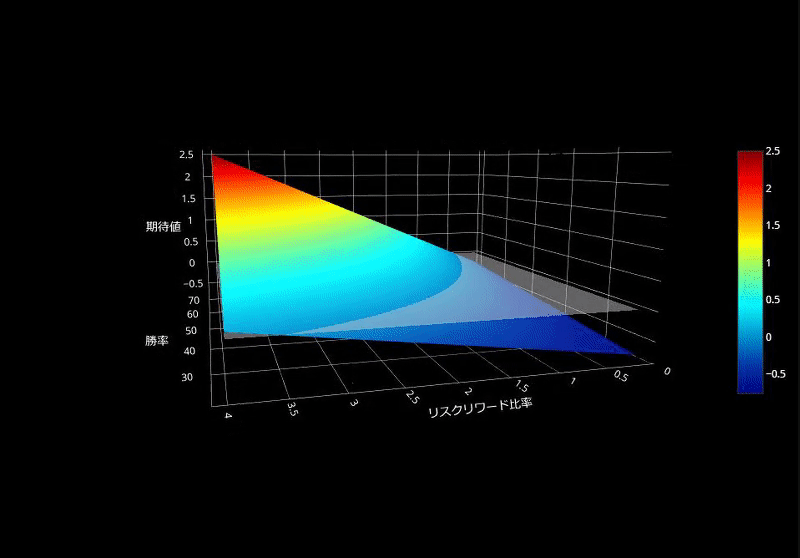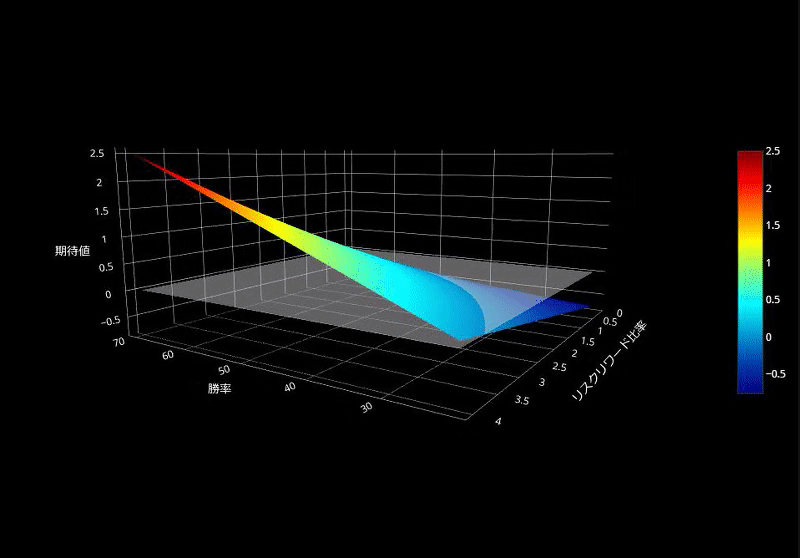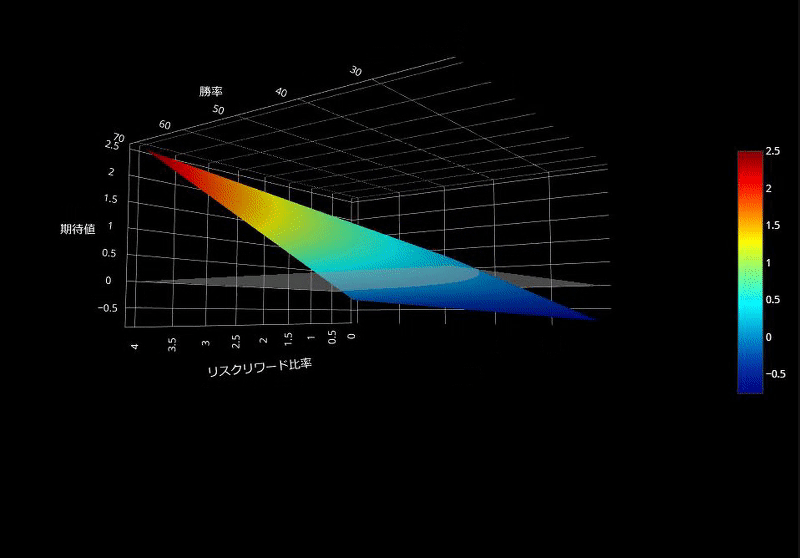
損益分岐点をトレードで用いる際の注意点
さて、ここまで説明してきた「損益分岐点」と「期待値」ですが、実はトレードで用いる際にはいくつかの注意点があります。他の記事の紹介を交えながら、説明をしていきます。
単利運用が条件
投資をする上で、「単利」と「複利」という運用方法があります。ここまでご説明してきた「損益分岐点」や「期待値」はすべて「〝単利〟を前提としたもの」です。この点を認識していないと、「勝てるはずなのに、なぜか負けてしまった」という事態が起こります。
それは「複利の罠」によるものなのですが、説明をするには少し長くなるので、「何のことか検討もつかない」という方は以下の記事を読むと良く分かると思います。
資金管理をしなければならない
これは「破産の確率」によるものです。
例えば「勝率50%、RR比2倍」の手法があるとして、これは「損益分岐点」で考えると間違いなく「勝てる手法」です。しかし、勝率が50%だということは「負けトレードも50%ある」ということです。しかも交互に勝って負けるわけではなく「連敗」があります。勝率50%なら、最低でも「『5連敗』はよくある」と想定しておく必要があります。
ここで問題になるのは、1トレードにとるリスクです。元金100万円で、毎回50万円のリスクで取引してしまえば、とても「5連敗」には耐えられません。
「5連敗」に耐えるには、1トレードのリスクを「20万円」まで下げる必要があるのですが、実際のトレードにおいてはそれでも十分ではありません。
これ以上は長くなるので割愛しますが、「よくわからん」な方は以下の記事をお読みください。この話は、意外とトレードをする上で「軽視されがちで最も重要なポイント」です。
トータルプラス ≠ 破産しない
「損益分岐点」とは、トータルがプラスかマイナスかを見ています。しかし、そこには連敗などの概念はなく、「破産するかどうか」はまったく別の話です。試していただきたいのですが、「損益分岐点」は収益で考えれば「±0」ですが、実は「破産の確率」は「90%以上」になります。
つまり、ここから分かる以下の2点を認識しておかなければいけません。
- 「『損益分岐点』では不十分」(そもそも投資をしていて±0では物足りないですが・・)
- 「『破産の確率』が1%未満の手法であれば、おそらく収益もプラスである」
複利の場合はどうなるのか
この記事を書いている間に、すごく良い記事をみつけてしまいました。
これまで、ボクは〝単利〟の「損益均衡点」や「期待値」の算出方法しか知らなかったのですが、〝複利〟の「損益均衡点」を算出している方がいました。2006年の記事ですが、良い記事です。
少し引用してみます。
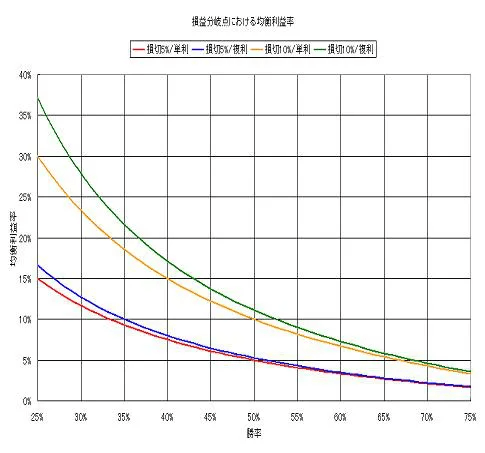
通常のトレードでは、損切りを行うことで損失(率)をコントロールすることができる。あとは、勝率が決まれば損益分岐点となる利益率(均衡利益率)を決定することができる。
それは、平均リターンと複利リターンの場合で異なり、それぞれ次式で計算できる。
[平均リターン]:均衡利益率=(1-勝率)*損失[損切]率/勝率
[複利リターン]:均衡利益率=(1-損失[損切]率)^(1-1/勝率)-1これらを損失[損切]率をパラメータとしてチャートにすると、下図のようになる。なお、チャートは勝率25%~75%の範囲で表示している。
上記を元に、同じグラフを再現することができました。
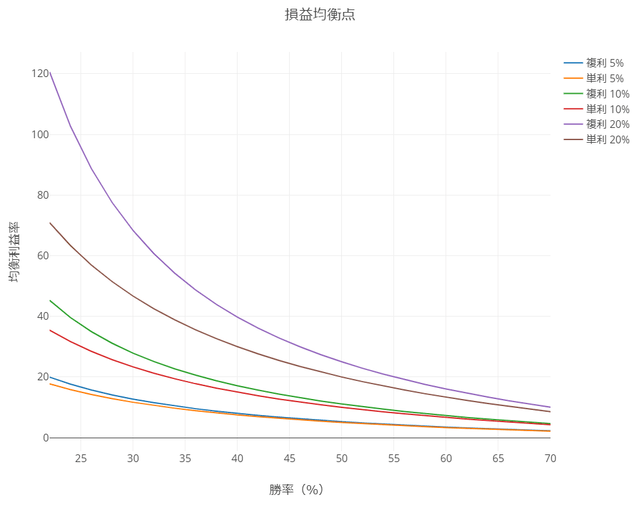
このグラフから、「複利運用下で同じ勝率」だとすると「利益を大きくとらないといけない」ということがわかります。
- 勝率40%のときに均衡するためのRR比
- 単利:15% / 10% = RR比 1.5倍
- 複利:17.12% / 10% = RR比 1.712倍
残念ながら、〝複利〟の計算には元金が絡むため、「〝単利〟のように『期待値』を算出すること」はちょっと難しそうです。でも、〝複利〟の「損益均衡点」が分かるだけでも「やるべきこと」が明確になります。
注意点で「〝単利〟が条件」と書きましたが、別に「〝複利〟が悪い」というわけではありません。
〝複利〟の方が危険。
その危険度が「どれくらいなのか」を知る必要があるということです。

- 記事をシェア