どんな記事
Google Colab および Python で「『破産の確率』を算出する方法」「破産確率表の作成」「破産確率表のグラフ化」「破産の確率の計算式とコードの解説」などを備忘録としてメモ。
破産の確率は、勝率、リスクリワード比率、リスクの許容などの項目から算出する。
コードを公開しているので、Google Colabにコピペで再現できます。
この記事のコードで計算すると、以下リンク先の「『破産の確率』計算機」と同じ算出結果になる。
〝破産の確率〟計算機 - Investment Tech Hack
〝破産の確率〟の計算ツール。項目と活用している方法の解説もあります。「破産を防ぐ5つのポイント」「破産せずに利益を最大化する3つのポイント」「最短で投資の管理・分析を実現するGoogleシート」など。
investment.abbamboo.com

追記・修正
2019年1月30日 修正
「〝定額〟の「破産の確率」を算出する」「〝定率〟の「破産の確率」を算出する」のコードを修正。
2019年1月30日 追記
「破産確率表を算出して3Dのグラフを描画する」「「破産の確率」の計算式とコードの解説」を追記。
〝定額〟の「破産の確率」を算出する
定額 ≒ 単利
import numpy as np
win_pct = 0.38 # 勝率
risk_reward = 2.09 # リスクリワード比率
risk_rate = 0.05 # 1回のトレードで取るリスク率
class ruin_fixed_amonunt():
def __init__( self ,win_pct ,risk_reward ,risk_rate ):
self.win_pct = win_pct
self.risk_reward = risk_reward
self.risk_rate = risk_rate
if self.is_error() : raise
def is_error( self ) :
if self.win_pct == 0 \
or self.risk_reward == 0 \
or self.risk_rate == 0 :
return True
elif not 0 <= self.win_pct <= 1 \
or not 0 < self.risk_reward \
or not 0 <= self.risk_rate <= 1 :
return True
else :
return False
def equation( self ,x ,P ,R ) :
return P * x**( R + 1 ) + ( 1 - P ) - x
def solve_equation( self ) :
S ,P ,R = 0 ,self.win_pct ,self.risk_reward
while self.equation( S ,P ,R ) > 0:
S += 1e-4
if S >= 1 : S = 1
return S
def calc( self ) :
S = self.solve_equation()
return S ** ( 1 / self.risk_rate )
if __name__=='__main__' :
ruin_rate = ruin_fixed_amonunt( win_pct ,risk_reward ,risk_rate ).calc()
print( f"破産確率(定額)は{ ruin_rate :.2%}です" )破産確率(定額)は3.87%です〝定率〟の「破産の確率」を算出する
定率 ≒ 複利。定率の場合は項目が増える。
import numpy as np
win_pct = 0.38 # 勝率
risk_reward = 2.09 # 損益レシオ
risk_rate = 0.05 # 1回のトレードで取るリスク率
funds = 1000000 # 初期資金
ruin_line = 200000 # 撤退ライン(破産)
class ruin_fixed_rate():
def __init__( self ,win_pct ,risk_reward ,risk_rate ,funds ,ruin_line ):
self.win_pct = win_pct
self.risk_reward = risk_reward
self.risk_rate = risk_rate
self.funds = funds
self.ruin_line = ruin_line
if self.is_error() : raise
def is_error( self ) :
if self.win_pct == 0 \
or self.risk_reward == 0 \
or self.risk_rate == 0 \
or self.ruin_line == 0 :
return True
elif not 0 <= self.win_pct <= 1 \
or not 0 < self.risk_reward \
or not 0 <= self.risk_rate <= 1 \
or self.funds < 0 \
or self.ruin_line < 0 \
or self.ruin_line > self.funds :
return True
else :
return False
def equation( self ,x ,P ,R ) :
return P * x**( R + 1 ) + ( 1 - P ) - x
def solve_equation( self ,win_pct ,R ) :
S ,P = 0 ,win_pct
while self.equation( S ,P ,R ) > 0:
S += 1e-4
if S >= 1 : S = 1
return S
def calc( self ) :
a = np.log( 1 + self.risk_reward * self.risk_rate )
b = abs( np.log( 1 - self.risk_rate ) )
n = np.log( self.funds / self.ruin_line )
R = a / b
S = self.solve_equation( self.win_pct ,R )
return S ** ( n / b )
if __name__=='__main__' :
ruin_rate = ruin_fixed_rate( win_pct ,risk_reward ,risk_rate ,funds ,ruin_line ).calc()
print( f"破産確率(定率)は{ ruin_rate :.2%}です" )破産確率(定率)は2.46%です破産確率表を算出して3Dのグラフを描画する
必要なモジュールのインストールと読み込み
# Plotly のインストール
!pip install plotly --upgradeimport pandas as pd
import plotly
import plotly.graph_objs as go
import plotly.figure_factory as ff
plotly.offline.init_notebook_mode( connected=True )
# google colabでplotlyを表示するにはこれが必要。
# グラフを書き出すセルごとに使用する
def enable_plotly_in_cell():
import IPython
from plotly.offline import init_notebook_mode
display(IPython.core.display.HTML('''
<script src="/static/components/requirejs/require.js"></script>
'''))
init_notebook_mode( connected=False )破産確率表の算出
win_range = np.arange(0.3 ,0.62 ,0.005)
rr_range = np.arange(0.4 ,3.1 ,0.025)
risk_rate = 0.02
funds = 1000000
ruin_line = 200000
df_ruin = pd.DataFrame()
for win in win_range :
for rr in rr_range :
ruin_rate = ruin_fixed_rate( win ,rr ,risk_rate ,funds ,ruin_line ).calc()
df_ruin.loc[ rr ,win ] = ruin_rate
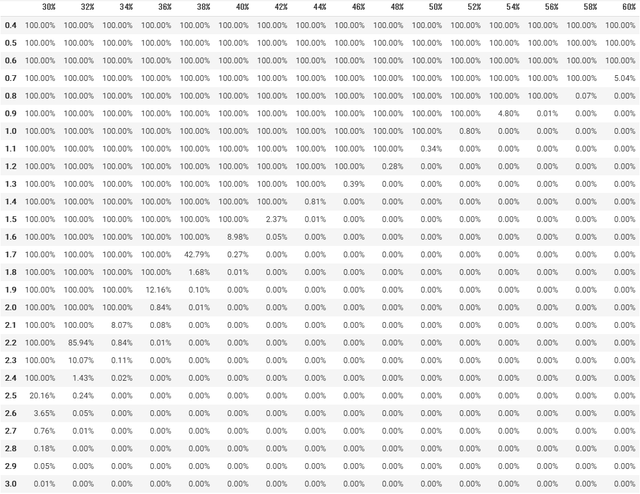
df_ruin破産確率表をもとに3Dのグラフを描画する
計算量が多いので、やや時間が掛かります。
layout = go.Layout( title = f'定率、損失の許容:{risk_rate}、元金{funds/10000:.0f}万円、破産の基準:{ruin_line/10000:.0f}万円'
, autosize = False
, paper_bgcolor = "#000"
, width = 1000
, height = 800
, scene = dict(
aspectmode = "manual"
, aspectratio = dict(x=1 ,y=1 ,z=0.5)
, xaxis = dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,title="勝率")
, yaxis = dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,title="リスクリワード比率")
, zaxis = dict(color="#fff" ,linecolor="#fff" ,gridcolor="#eee" ,title="破産の確率")
, camera = dict(eye=dict(x=2 ,y=1.25 ,z=1.5)) )
, font = dict(color="#fff") )
z1 = df_ruin
data = [ go.Surface( z = z1.T
, y = z1.index
, x = z1.columns
, cmin=0 ,cmax=1
, colorscale = "Jet"
, colorbar = dict(lenmode='fraction', len=0.5)
, contours = dict(x=dict(color="#fff") ,y=dict(color="#fff") ,z=dict(color="#fff")) ) ]
enable_plotly_in_cell()
plotly.offline.iplot( go.Figure( data=data ,layout=layout ) )計算式とコードの解説
ここからは、参考にしたサイトから引用しながら、「破産の確率」の計算式とコードについて解説していきたいと思います。計算式については、元のサイトより分かりやすく説明できる自信がないため、コードの解説が主になるかもしれません。ややこしい話なので興味がない方はスルーしちゃってください。
まずシンプルに考える
まずは、引用を。一部、省略したりしています。
<問題>
勝つと a 円もらえ、負けると b 円失う賭がある。勝つ確率を P とする。あなたは、現在、n 円持っている。この賭を際限なく繰り返すとき、破産する(所持金が0以下になる)確率はいくらか。※ 最後に借金が残る場合もありえます。たとえば、a=15、b=10、n=10 のとき、「勝ち(25円)→ 負け(15円)→ 負け(5円)→ 負け(-5円)」となれば、5円の借金をかかえて破産です。
引用元: ¥∞:破産の確率
これ以降、引用の中にでてくる「a、b、P、n」などはすべて同じものを指しています。(利益=a など)
P ≦ (a+b) のときは、「1回あたりの期待値≦0」 なので、やるだけ無駄です。この場合、破産の確率は 「1」で、際限なくやっていれば必ず破産します。そこで、以下では P > b / (a+b) とします。
a=b で、n/b が整数の場合、破産の確率は次のようになる。
実際に数字を入れて計算してみると以下のようになる。
例)Aさんは、資金 200万円で株をやっている。トレード1回ごとの勝率は 60%で、勝つときは 10万円儲け、負けるときは 10万円損をする。Aさんの破産の確率はいくらか。
前述の「a、b、P、n」に当てはめ、「a=b=10、n=200、P=0.6」として計算したもの。これだと「a=b で、n/b が整数の場合」という条件があり不十分。
定額の「破産の確率」を計算する
ここで引用元のサイトの方も行き詰まったようです。
というわけで、a=b の場合は簡単です。そうでないときは、どうするのか?
a と b が異なる整数の場合、数式は書き出せるのですが、高次方程式の解��(それも複素数の解)を求める必要があり、実用的でありません。簡単な近似式がないものかと少し考えてみたのですが、わかりませんでした。
そこで近所の図書館へ行き、『確率論とその応用』という本(W・フェラー著、確率論の名著らしいです)を借りてパラパラ見てみると …。ありました!!さすがに名著といわれるだけのことはあります(笑)
引用元: ¥∞:破産の確率
ここでついに、欲しかった計算式がでてきます。
フェラーの本に出ている式に少し手を加えることで、次のように結論できます。
まず損益比 R を R=a/b で定義します。
0<x<1 の範囲における、次の方程式の解を S とします(この範囲における解は1つしかありません)。このとき、次の評価式が成立します。
n/b と R がともに整数の場合は、右辺の等号が成立します。つまり、破産の確率=S^(n/b) です。
※ この評価式の証明は、数学の素養があればそれほど難しくありません。知りたい人は、フェラーの本を見てください。フェラーの 『確率論とその応用』 は、「1」 と 「2」 があり、それぞれ上巻・下巻に分かれています(つまり全4巻)。この評価式は、「1」 の下巻、461ページにある式(8・12)から導くことができます。
ここまでを関数化したのが、定額の「破産の確率」を求めるruin_fixed_amonunt()です。
「〝定額〟の「破産の確率」を算出する」と見比べながらお読みいただきたいのですが、def equation( self ,x ,P ,R )のP * x**( R + 1 ) + ( 1 - P ) - xが上記の方程式を表しています。これをsolve_equation()で解いているわけです。具体的には、数字を代入しまくって近い数字を探しています。
そして、方程式から求めた「S」を元にS ** ( 1 / self.risk_rate )で「破産の確率」を求めています。
定率の「破産の確率」の計算
さて、賭け金を一定にするのではなく、資金に対して一定の比率で賭けていく場合はどうでしょうか。
つまり、その時点の資金を A 円とするとき、一定の比率 k (0<k<1)を用いて、勝てば R×k×A 円儲け、負ければ k×A 円損するように賭けるとします。
※ たとえば、損益比 R(=利益÷損失)が 2 とします。k=0.1 なら、常に資金の 10%をリスクにさらします。資金 100万円なら、負けは 10万円の損、勝ちは 20万円の得となるように賭け、それに勝って資金が 120万円になれば、次は、負けは 12万円の損、勝ちは 24万円の得となるように賭けるわけです。
はじめの資金を A₀円とし、資金が B 円以下になったら破産とします。
W 回勝って、L 回負けたとき、資金が B 円以下になって破産する条件は、次の式です。対数をとって変形すると次のようになります。
a、b、n を次のように定義します。
そうすると上の式は
と同じことです。
結局、この問題は 「資金が n 円、勝つと a 円儲け、負けると b 円失うときの破産の確率は?」 と同じです。つまり、このページのはじめの <問題> に還元されるわけです。上に書いた確率の評価式は、a、b、n が整数でなくても成立するので、それを適用すれば評価が出せます。
引用元: ¥∞:破産の確率
と、ここで引用元の記事は終わっています。
これは、「定率にしたことで『a、b、n』の考え方は変わったけど、全体の考え方は一緒だよね」ということです。つまり、あらたな『a、b、n』を定額の計算式に代入してあげれば「定率の『破産の確率』」を算出することができます。
この説明を踏まえて「〝定率〟の「破産の確率」を算出する」をみてみると、ruin_fixed_rate()の全体の構成がruin_fixed_amount()�とほぼ同一であることが分かると思います。〝定率〟の計算式は、〝定額〟のそれに項目を追加し、定率用の「a、b、n」を別途算出すれば、あとは同様の計算で良いわけです。
開発を承っています
- Pineスクリプト(インジケーターやストラテジー)
- Google Apps Script
- Python
- MQL4
などの開発を承っています。とくに投資関連が得意です。過去の事例は「実績ページ(不定期更新)」でご確認ください。ご相談は「お問い合わせ」からお願いします。

- 記事をシェア