どんな記事
- リスクをとれば利益が増える
- リスクをとりすぎると破産する
破産しない範囲�の最大のリスクを確認することで、資金効率の良い投資ができるようになります。
この記事の〝最大リスク表〟を確認すると、素早く〝最大リスク〟を確認することができます。
効率の良い投資
破産しない範囲の最大のリスクで運用していく
筆者は、これが最も〝投資効率の良い投資〟だと考えています。
リスクとリターンは表裏一体ですから、リスクをとった方がリターンは大きくなります。一方で、リスクを取り過ぎてしまうとあっという間に破産します。
〝最大のリスク〟というと何だか怖そうですが、「破産しない範囲でリターンを追求しましょう」ということです。
破産する確率は計算できる
このサイトでもWebツールを用意していますが、〝破産してしまう確率〟は計算することができます。
- 勝率
- 利益と損失の割合
- どれくらいのリスクをとるか
といった数値があれば算出できるので、用意するデータのハードルも高くありません。
入試問題になることもあり数学ではメジャーな題材のようです。
〝破産の確率〟計算機
〝破産の確率〟の計算ツール。項目と活用している方法の解説もあります。「破産を防ぐ5つのポイント」「破産せずに利益を最大化する3つのポイント」「最短で投資の管理・分析を実現するGoogleシート」など。
investment.abbamboo.com

リスクとリターンは表裏一体
サイコロに置き換えると分かりやすいのですが、
- 1~5の目が出たら 100% の利益
- 6の目は 100% の損失(全額を失う)
6分の5の確率で勝てますが、6の目が一度でもでると破産します。こういう投資の〝破産の確率〟は100%です。
これは「83%の勝率で100%のリスクをとっている」という極端な例ですが、リスクを取り過ぎれば勝率が99%であっても破産します。
一方で、せっかく勝率が83%という条件の良い投資があっても、少ないリスクで運用しているとリターンが小さくなってしまいます。
- 1~5の目が出たら 1% の利益
- 6の目は 1% の損失
1%だと何だか物足りなくないですか?もうちょっとリスクをとっても良さそうですよね。
破産しない最大リスク
過去に「〝取引量と勝率〟が複利運用において最も重要」という記事で、次のような表を掲載しました。
勝率:80%、RR比:0.5の手法における破産の確率
| 2% | 8% | 9% | 26% | 27% | |
|---|---|---|---|---|---|
| 単利 | 0% | 0% | 0.01% | 3.24% | 3.68% |
| 複利 | 0% | 0% | 0% | 0% | 0.01% |
RR比というのは利益と損失の割合を表すもので、0.5は「利益が損失の半分である」ということです。
この表は「2~27%のリスク」や「単利と複利の違い」でどの程度の〝破産の確率〟になるかを算出したもので、単利運用かつ2~8%のリスクなら〝破産の確率〟はゼロだということが分かります。
「破産しないなら8%のリスクをとろうよ」
というのが、この記事の前提です。
これを 「破産しない最大リスク」 と表現しています。
この記事を書くにあたって、勝率とRR比を条件に「破産しない最大リスク」を網羅的に算出しました。
最大リスク表
以下の条件で作成しました。
- 勝率:30~60%
- RR比:0.4~2.8倍
- 破産の確率が0.1%未満の最大リスク
- 定率(複利)は元手100万円、破産の基準20万円
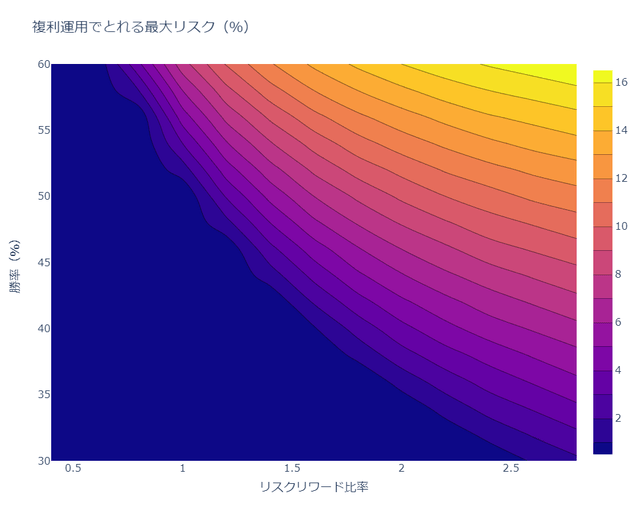
グラフ
グラフで確認すると全体感がよく分かります。
- 青はリスクが取れないエリア
- 黄色になるほど大きなリスクをとれる
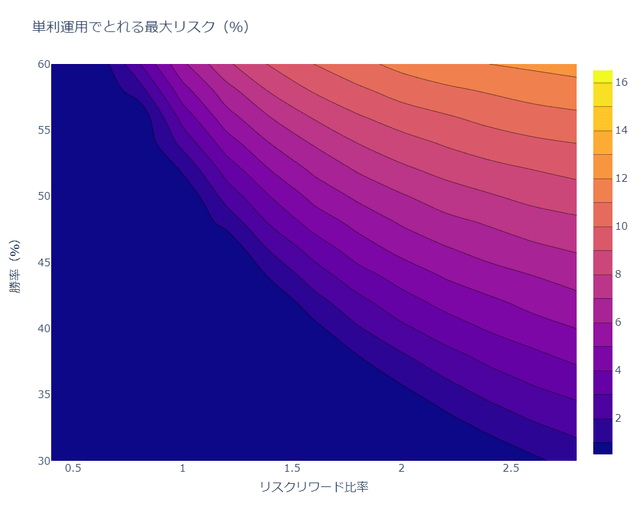
- 複利運用の方が大きくリスクをとれる
数値の一覧表
複利運用の最大リスク表
| 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | 2.6 | 2.8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60% | 0.0 | 0.0 | 3.8 | 7.6 | 10.1 | 11.9 | 13.2 | 14.2 | 15.0 | 15.6 | 16.1 | 16.5 | 16.9 |
| 58% | 0.0 | 0.0 | 2.0 | 6.0 | 8.7 | 10.6 | 12.0 | 13.0 | 13.8 | 14.5 | 15.0 | 15.4 | 15.8 |
| 56% | 0.0 | 0.0 | 0.3 | 4.5 | 7.3 | 9.2 | 10.7 | 11.8 | 12.6 | 13.3 | 13.9 | 14.3 | 14.7 |
| 54% | 0.0 | 0.0 | 0.0 | 3.0 | 5.9 | 7.9 | 9.4 | 10.6 | 11.5 | 12.2 | 12.8 | 13.3 | 13.7 |
| 52% | 0.0 | 0.0 | 0.0 | 1.5 | 4.5 | 6.6 | 8.2 | 9.4 | 10.3 | 11.1 | 11.7 | 12.2 | 12.6 |
| 50% | 0.0 | 0.0 | 0.0 | 0.0 | 3.1 | 5.3 | 7.0 | 8.2 | 9.2 | 10.0 | 10.6 | 11.2 | 11.6 |
| 48% | 0.0 | 0.0 | 0.0 | 0.0 | 1.7 | 4.0 | 5.8 | 7.1 | 8.1 | 8.9 | 9.6 | 10.1 | 10.6 |
| 46% | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 2.7 | 4.5 | 5.9 | 7.0 | 7.8 | 8.6 | 9.1 | 9.6 |
| 44% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.5 | 3.3 | 4.8 | 5.9 | 6.8 | 7.5 | 8.1 | 8.6 |
| 42% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 2.1 | 3.6 | 4.8 | 5.7 | 6.5 | 7.1 | 7.7 |
| 40% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.9 | 2.4 | 3.7 | 4.7 | 5.5 | 6.1 | 6.7 |
| 38% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 2.6 | 3.6 | 4.4 | 5.1 | 5.7 |
| 36% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 1.4 | 2.5 | 3.4 | 4.1 | 4.8 |
| 34% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 1.4 | 2.4 | 3.1 | 3.8 |
| 32% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.4 | 1.3 | 2.1 | 2.8 |
| 30% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 1.1 | 1.8 |
単利運用の場合
| 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | 2.2 | 2.4 | 2.6 | 2.8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 60% | 0.0 | 0.0 | 2.9 | 5.8 | 7.8 | 9.1 | 10.0 | 10.7 | 11.3 | 11.7 | 12.0 | 12.2 | 12.4 |
| 58% | 0.0 | 0.0 | 1.5 | 4.6 | 6.6 | 8.1 | 9.1 | 9.8 | 10.4 | 10.8 | 11.1 | 11.4 | 11.6 |
| 56% | 0.0 | 0.0 | 0.2 | 3.4 | 5.6 | 7.0 | 8.1 | 8.9 | 9.5 | 9.9 | 10.3 | 10.6 | 10.8 |
| 54% | 0.0 | 0.0 | 0.0 | 2.3 | 4.5 | 6.0 | 7.1 | 8.0 | 8.6 | 9.1 | 9.5 | 9.8 | 10.0 |
| 52% | 0.0 | 0.0 | 0.0 | 1.1 | 3.4 | 5.0 | 6.2 | 7.1 | 7.8 | 8.3 | 8.7 | 9.0 | 9.3 |
| 50% | 0.0 | 0.0 | 0.0 | 0.0 | 2.4 | 4.0 | 5.3 | 6.2 | 6.9 | 7.5 | 7.9 | 8.3 | 8.5 |
| 48% | 0.0 | 0.0 | 0.0 | 0.0 | 1.3 | 3.1 | 4.4 | 5.3 | 6.1 | 6.7 | 7.1 | 7.5 | 7.8 |
| 46% | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 2.1 | 3.4 | 4.5 | 5.3 | 5.9 | 6.4 | 6.8 | 7.1 |
| 44% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.1 | 2.5 | 3.6 | 4.4 | 5.1 | 5.6 | 6.0 | 6.4 |
| 42% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 1.6 | 2.7 | 3.6 | 4.3 | 4.8 | 5.3 | 5.7 |
| 40% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.7 | 1.9 | 2.8 | 3.5 | 4.1 | 4.6 | 5.0 |
| 38% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.9 | 2.7 | 3.3 | 3.8 | 4.3 |
| 36% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 1.1 | 1.9 | 2.6 | 3.1 | 3.5 |
| 34% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 1.1 | 1.8 | 2.4 | 2.8 |
| 32% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.3 | 1.0 | 1.6 | 2.1 |
| 30% | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.2 | 0.8 | 1.4 |
最大リスクの活用
〝破産しない最大リスク〟が分かれば、それを基準にした取引量を算出することができます。過去の記事で詳しく解説しているので、ご覧ください。
破産せずに利益を最大化する3つのポイント
ある検証結果があるときに、「何回トレードするとどれくらいの利益になるのか」や「そのトレードルールと自分の投資金でどの程度のリスクをとっていいのか」がわかるようになります!
mesure-the-risk/hasan-kakuritsu4

「期待値」と「大数の法則」まとめ
筆者が持つ「期待値」と「大数の法則」の全情報を掲載します。また、「『期待値』と『大数の法則』を投資に活かす具体例と注意点」にも触れています。大げさではなく、不動産なども含め、株やFX、すべての投資で重要な法則です。
mesure-the-risk/trading-edge-and-law-of-large-numbers

06.〝取引量と勝率〟が複利運用において最も重要
複利運用には勝率の高い手法が有利で、勝率の低い手法においては取引量の調整が非常に重要です。その根拠と、破産の確率を用いた取引量の調整について解説します。
take-advantage/compound-interest-6

注意点
〝破産の確率〟は役に立ちますが、注意点がいくつかあります。
- 実際の運用とは異なる
- 長期的な視野
- 投資信託とかは別の話
- 気にしないケースもある
〝破産の確率〟はあくまでもひとつの理論です。
「勝率やRR比が一定、リスクも均等」といった仮定の上に成り立っていて、実際の運用とは異なります。〝破産の確率〟が0%だったとしても絶対に破産しないわけではありません。
また、長期間に渡ってたくさんの売買を繰り返すような運用を想定しています。投資信託のように長期間保有し続けるようなものには当てはまりません。
「勝ち逃げできれば良い」
「少ない元本でスタートしているから全額なくなっても良い」
こういう前提で〝破産の確率〟を気にしないケースもあり得ます(限度はありますが)。
- 勝率やRR��比をできる限り信頼できるデータにする
- 資金管理を徹底してリスクを揃える
- 目安として使う
- 余裕を持った設定にする
- 期待値や損益分岐点等も併せて確認する
このように〝破産の確率〟を使うときには配慮が必要です。
データおよびグラフの作成
最大リスクの一覧表やグラフはGoogle Colaboratoryで作成しました。「Google Colab サンプル集」に置いておきますのでご覧ください。
まだ登録されていない方は以下からご登録いただけます。

- 記事をシェア