どんな記事
あれ、何でこんなに損切りが続いてるんだろう…?
投資をしていると、ふとこう思うことが(意外と)あります。
この記事では、統計学の視点から「投資における連敗の想定は何回が妥当なのか」 を考えていきます。あなたの投資で想定するべき連敗が「意外と多い」ことに少しビックリしてしまうかもしれません。
この記事を読めば、
- 想定すべき連敗の数
- それを踏まえた資金管理とリスク管理の仕方
- 損切りの目安にするべきテクニカル指標
などが、分かるようになります。
追記
2021年2月17日
「戦略は常に相場に依存する」を追記しました。
戦略は常に相場に依存する
BBBさんの意見に賛成です。正しいと思います。
まとめでも触れていますが、相場に合わせて戦略を生むべきであって、勝率から想定される連敗数からロジックを作るのは誤ったアプローチだと思います。
この記事の内容はひとつの目安としてお読みください。
結論:想定するべき連敗
いきなりですが、結論です。
最低でも、以下の連敗数を想定するべきだと考えます。
株式投資やFXをする上で、「何回の連敗を想定すれば良いのか」だけが知りたい方は、ここを読んでいただけば事足ります!
根拠や注意点、連敗の想定を活かした資金管理とリスク管理が知りたい方は、どうぞ先まで読み進めてください。
| 勝率 | 想定するべき連敗 |
|---|---|
| 30% | 9連敗 |
| 40% | 6連敗 |
| 50% | 5連敗 |
| 60% | 4連敗 |
| 70% | 3連敗 |
「絶対、確実に」この連敗でおさまるわけではありませんが、「ほぼ(約95%の確率で)この範囲におさまるでしょう」 というものです。
統計学:予言的中区間
今回、連敗を推し量るにあたって、小島寛之先生の 「95パーセント予言的中区間」 という考え方を用いています。
参考にした本:統計学入門
「95パーセント予言的中区間」とは、95%でその範囲内におさまるという区間のことで、「完全独習 統計学入門(小島 寛之 著)」に掲載されています。
この**「95パーセント予言的中区間」は統計的推論のひとつ** で、小島先生は著書で次のように触れています。
統計的推論というのは、20世紀になって初めて確立された技術で、これは人類が待望していた方法論だといっていいのです。なぜならば、これは「部分的事実から全体についての推論を行う」という「帰納的推論」だったからです。
(中略)
「昨日までずっと何千年にもわたって太陽は昇り続けた。だから、明日からもずっと太陽は昇るだろう」という**「部分から全体へ」**という形式の推論になります。
引用元 統計学入門 P.98
30年近くファンド運用に携わっていた方 とお話をする機会があり質問したことがあるのですが、その方は 「ファンド運用はすべて統計学にもとづいて行っていた」 とお話されていました。
例題:コイントスと95パーセント予言的中区間
「完全独習 統計学入門(小島 寛之 著)」から、「95パーセント予言的中区間」の例題についてひとつ抜粋します。
「N枚のコイン投げで出る表の枚数」は近似的に「平均値がN/2でS.D.(標準偏差:データのばらつき)が√N/2の一般正規分布」になります。例えば「100枚のコインを同時に投げたときに出る表の枚数」を多数回繰り返し観察して相対度数のヒストグラムを作成すると、
「平均値が100/2=50でS.D.が√100/2=5の一般正規�分布」のヒストグラム
とほとんどそっくりのものができることが知られています。さて、あなたが今から100枚のコインを同時に投げるとして、出る表の枚数を予言するとき、「95パーセント予言的中」になる範囲を作ってみることにしましょう。
先ほど紹介した法則より、「(μー1.96σ)以上(μ+1.96σ)以下(μ:平均、σ:標準偏差)」を予言すればいいわけですから、μ=50、σ=5を代入すればよく、
「(50-1.96✕5)以上(50+1.96✕5)以下」=「40.2以上59.8以下」
が95パーセント予言的中範囲となります。つまり、「40枚から60枚が表になる」と予言しておけば、おおよそこの予言は当たります。引用元: 統計学入門 P.86
このように、95%の的中範囲を算出することができる のです。
ちなみに、この考え方はボリンジャーバンドでよく言われるものですよね。意外と、馴染み深いインジケーターで、あたり前のように使われている考え方なのです。
ボリンジャーバンドでは「±2σに95.5%の確率でおさまる」としていますが、統計学では「きっちり95%とするために±1.96σとする」のが慣習なのだそうです。
(本当は細かい条件がありますが、基本的には)ある事象の平均と標準偏差を知ることができれば、
平均 ± 1.96 ✕ 標準偏差
で、的中率95%の予言が可能
つまり、こういうことが成り立つわけです。
細かい説明は割愛していますので、ご興味がある方はぜひ「完全独習 統計学入門(小島 寛之 著)」をお読みください。非常にわかりやすく解説されています。
応用:連勝と連敗
今回の検証は、Pythonで行いました。
「Pythonの導入~投資のデータ分析でどういうことができるか」については、以下で詳しく解説しています。ご覧ください。
さて、ここでは「連敗を予言する手順」を実際に使用したpyhtonのコードとともにご紹介していきます。
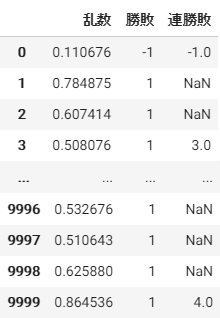
まず、0~1のランダムな数値を1万個作成し、数値に対して「勝ち」「負け」を分類します。ここでは、0.5より大きいものを勝ちとして「勝率50%の場合」の検証を行っています。
df1 = pd.DataFrame(np.random.rand(10000) ,columns=["乱数"])
df1["勝敗"] = df1.apply(lambda x : 1 if x["乱数"] > 0.5 else -1 ,axis=1)さらに、できたデータの「連勝」と「連敗」をカウントします。
for i in range(len(df1)) :
if i == 0 :
df1.loc[i ,"連勝敗"] = df1.loc[i ,"勝敗"]
else :
I = df1.loc[i ,"勝敗"]
I_ = df1.loc[i-1 ,"連勝敗"]
if I == 1 and I_ < 0 :
df1.loc[i ,"連勝敗"] = int(1)
elif I == -1 and I_ > 0 :
df1.loc[i ,"連勝敗"] = int(-1)
else :
df1.loc[i ,"連勝敗"] = int(I + I_)
df1.loc[i-1 ,"連勝敗"] = np.nanすると、こういうデータができあがります。ここでは連敗をマイナスとして扱っています。
このデータに対して統計をとります。
df1_describe = df1["連勝敗"].dropna().describe()count 5024.000000
mean -0.013933
std 2.432813
min -12.000000
25% -2.000000
50% 0.000000
75% 2.000000
max 11.000000
Name: 連勝敗, dtype: float64この結果から、次のような特徴が読み取れます。
- 乱数を1万個作成し、その「連勝敗」をカウントすると5024例になった
- 平均(mean)はほぼゼロ(勝率50%で連敗をマイナスとしているから平均をとるとゼロになります)
- データのばらつき(std:標準偏差)は2.43
- 連敗でもっとも回数が多かったものは12連敗
- 連勝で最大は11連勝
この統計から平均と標準偏差がわかりましたので、「95パーセント予言的中区間」を導き出すことができるわけです。
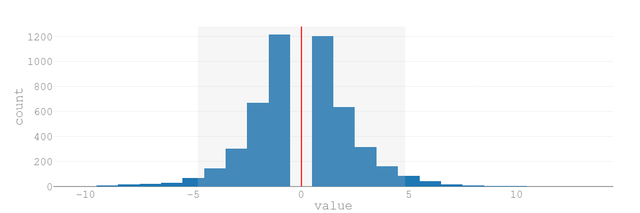
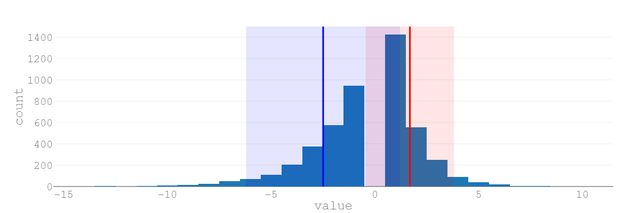
以下が、そのグラフです。
赤いラインが平均。横軸が「連勝敗の数」(2連勝、3連敗など)、縦軸が各連勝敗が起こった数、そして、グレーの網掛けが「95パーセント予言的中区間」を表しています。
「5連敗~5連勝」がおよそ95%の確率で起こる
よって、「最低限想定するべき連敗は5回」という結論になる わけです。
ただし、この数を鵜呑みにするのは大変危険 です。注意点がありますので、以下に記載する「連敗を想定した資金管理」も必ずお読みください。
結論の詳細:勝率ごとの想定すべき連敗の数
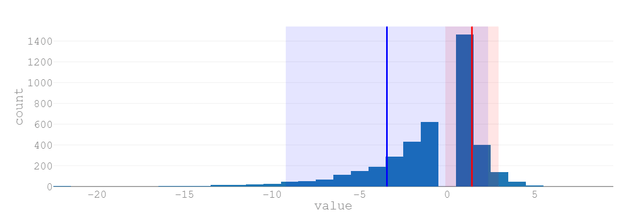
以下に、勝率60%、70%、40%、30%のデータを掲載します。
あなたがもし、「自分は損切りばかりだなあ」と思っているとしたら、ぜひ、この�「想定するべき連敗の数」を参考にしてください。
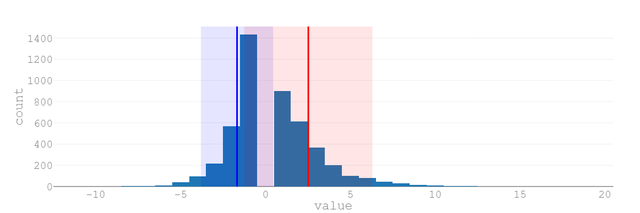
勝率60%
| 想定すべき連敗の数 | 4回 |
| 連敗の平均回数 | 1.67回 |
| データのばらつき | 1.09回 |
| 最大連敗数 | 12回 |
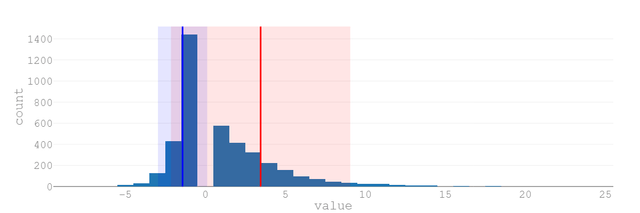
勝率70%
| 想定すべき連敗の数 | 3回 |
| 連敗の平均回数 | 1.42回 |
| データのばらつき | 0.79回 |
| 最大連敗数 | 9回 |
勝率40%
| 想定すべき連敗の数 | 6回 |
| 連敗の平均回数 | 2.49回 |
| データのばらつき | 1.91回 |
| 最大連敗数 | 15回 |
勝率30%
| 想定すべき連敗の数 | 9回 |
| 連敗の平均回数 | 3.44回 |
| データのばらつき | 3回 |
| 最大連敗数 | 22回 |
連敗を想定した資金管理
さ��て、「想定すべき連敗の数」についてはご理解いただけたと思います。
これが分かると、次のようなリスクの管理をすることができるようになります。(注意:これだけでは完璧じゃないので、必ず最後までお読みください)
- 基本的な損切りのスキームを必ず決める
- 「損切りの幅 ✕ 想定するべき連敗の数」が、自分の資産額を超えないようにする
これをイメージしながら取引をすれば、かなり連敗に強くなると思います。
しかし、実は、このリスク管理だけでは不十分 です。つまり、これだけでは投資で壊滅的なダメージを負ってしまう可能性があります。
なぜか――
それは、「最大の連敗数」が考慮されていない からです。
あなたが、仮に1年や2年しか投資をしないとしたら、「最大の連敗数」を考慮する必要はあまりありません。
しかし、もし、あなたが生涯投資をしながら暮らしていくとしたら、何十年も投資を続けていくのだとしたら、「95パーセント予言的中区間」が外れて、とんでもない連敗(最大の連敗数)を喰らってしまう、資産が一気に尽きてしまう 可能性があるのです。
そもそも、「最大の連敗数」はあくまでもたかだか1万例の結果であって、それ以上の連敗の可能性も(限りなくゼロに近いですが)あります。
とすると、「最大の連敗数」を考慮した資金管理 をする必要があります。
それには、「95パーセント予言定期中区間」を参考にするのではなく、(これも同じく統計学の)「破産の確率」 という概念を用いて、ATRというテクニカル指標 をつかった資金管理とリスク管理をしていくのが最善であると考えています。
まとめ
この記事では、「勝率ごとの想定するべき連敗の数」を導き出してみました。
しかし、「連敗を想定した資金管理」で触れた通り、この検証結果だけで資金管理とリスク管理を決めてしまうのはすこし危険です。
一方で、勝率50%でも5連敗、勝率70%でも3連敗くらいは普通にあるものだと思っておくと、投資に挑む心構えが変わってくるはずです。

- 記事をシェア