どんな記事
このページには、
- ぼくがこれまで調べに調べ尽くした
- バックテストをする上でたくさんの研究もした
「期待値」の全情報 を掲載します。
また、投資に活かす〝具体例〟と〝注意点〟 にも触れています。
正直、「ここより詳しい『期待値』の情報はない」 と思います。
- 投資で思うような成果がでていない
- もっとロジカルに投資をしたい
- 投資の「期待値」についてちゃんと知りたい
こんな方にとって、この記事は大変役に立つものだと思います。
Twitterでも紹介していただいています
この記事で分かること
村上ファンドの村上世彰さんは、著書『生涯投資家』で次のように述べています。(村上さんは賛否あると思いますが有名な方です。知らない方は調べてみてください)
私の投資スタイルは、割安に評価されていて、リスク度合いに比して高い利益が見込めるもの、すなわち投資の「期待値」が高いものに投資をすることだ。投資判断の基本はすべて「期待値」にある。
いろいろな投資案件において、きわめて冷静に分析や研究をして、自分独自の「期待値」を割り出している。たとえば、百円を投資する場合の「期待値」の計算方法は、次のようになる。
- 0円になる可能性が20%、200円になる可能性が80%であれば、期待値は1.6(0×20%+2×80%=1.6)
- 0円になる可能性が50%、200円になる可能性が50%であれば、期待値は1.0
- 0円になる可能性が80%、200円になる可能性が20%であれば、期待値は0.4
期待値1.0を超えないと、金銭的には投資する意味がない。この「期待値」を的確に判断できることが、投資家に重要な資質だと私は考えている。
ちなみに多くの投資家は、0円になる可能性がある程度(20%以上)ある場合は、投資をしない。また、負ける確率が5割以上と考えた場合も投資しない(たとえば、5回投資して2勝3敗以下と予想される場合)。
このように、リスクが高い場合や勝率が低い場合には投資を避けるのが普通だが、「期待値」と勝率は別の概念だ。勝率が低いと言われる場合でも、自分なりの戦略を組み立てることで、勝率は変わらなくても、期待値を上げることはできる。
私の場合はすべてが「期待値」による判断なので、0円になる確率が5割を超えていても、勝率が1勝4敗でも、トータルリターンが1.0を大きく超えるかどうかで判断する。
引用元: 生涯投資家(村上世彰)
この記事を読むことで、この「期待値」が良く分かるようになります。
投資は〝ギャンブル〟か〝ビジネス〟か
ボクにとって、この答えはシンプルです。
長期的に、安定して収入が得られるなら〝ビジネス〟。そうでないなら〝ギャンブル〟。
さすがに宝くじで生活している人は知りませんが、世の中には世界のカジノを渡り歩く「プロギャンブラー」、パチンコで生計を立てる「パチプロ」など、ギャンブルと言われるものを生業として生活している人たちがいます。
長期的に、安定して収入が得られるのなら、〝ギャンブル〟であっても、それは〝�ビジネス〟 だと考えます。言うなれば「ビジネス的なギャンブル」でしょうか。
一方で、俗に言う〝ギャンブル〟よりもイメージの良い〝投資〟で、お金をどんどん溶かしてしまう人も多くいます。何百万、何千万と繰り返し損してしまう投資家もいます。もし、何度やってもそうなってしまうとしたら、それは「ギャンブル的な投資」です。
〝ギャンブル〟と〝投資〟、どちらにせよビジネス的に取り組もうとするときに必要となるのが 「期待値」 です。
「期待値」といえばテスタさん。「期待値」をもとにトレードをすることで有名です。また、cisさんも著書で「期待値」について触れています。
投資で、長期的に、安定して収入を得ようとするならば、「期待値」という概念を避けて通ることはできません。なぜなら、『期待値』を知らないと、しばしば投資判断を誤る からです。
「期待値」とは
例えば、ギャンブルにおいて掛け金に対して戻る金額の期待値とは、戻ってくる「見込み」の金額である。
引用元: Wikipedia:期待値
ここでは2つの例で「期待値」を解説してみたいと思います。
サイコロの「期待値」
例えば、次のような条件のゲームがあるとします。
- 100 円支払えば、6 面サイコロ 1 個を 1 回振ることができる
- サイコロの出た目に応じて次の賞金がもらえる
| 出た目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 賞金 | 20円 | 50円 | 100円 | 100円 | 150円 | 150円 |
このゲームの「期待値」は次のようにして求めることができます。
| 出た目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 賞金 | 20円 | 50円 | 100円 | 100円 | 150円 | 150円 |
| 確率 | 16.7% | 16.7% | 16.7% | 16.7% | 16.7% | 16.7% |
| 積 | 3.34円 | 8.35円 | 16.7円 | 16.7円 | 25.05円 | 25.05円 |
期待値 = 3.34 + 8.35 + 16.7 + 16.7 + 25.05 + 25.05 = 95.19円
計算してみると「期待値」は参加費 100 円より少なくなります。このことから、このゲームは平均的には1回あたり5円の損をし、回数を繰り返すほど損をするということが分かります。
このゲームを100回やり終わる頃には、参加費1万円に対して賞金は9,500円程度になることが考えられます。もちろん、回数が少ない場合はプラスになることもありますし、期待値以上の損になってしまうこともあります。
2つの封筒
これはあなたが「〝確率〟で考えるトレーダー」なのか、「〝期待値〟で考えるトレーダー」なのかが分かるゲームです。
- A と B の封筒がある
- どちらかの封筒は、もう一方の封筒の「倍の金額」が入っている
- あなたは A の封筒を受け取り、そこには「10,000円」が入っていた
- 相手の封筒(B)を確認することはできない
- あなたは「封筒の交換」を申し出ることができる
ぜひ、読み進める前に 「あなたならどうするか」 を考えてみてください。
ちなみに、ここで分かっているのは以下のことだけです。
相手の封筒(B)には、
- 50%の確率で 5,000円
- 50%の確率で 20,000円
さて、交換するのかしないのか「どちらを選べば良いか」は、「期待値」を算出してみるとすぐに分かります。
交換しない
交換する
「交換する場合」の方が良い期待値になることが分かりますね。
おそらく、勝てない投資家 の多くは「交換しない場合」を選んでしまいます。
なぜなら、「交換しない場合」は「10,000円の利益」が確定しているからです。相場に「確実さ」を求める〝勝率〟で考えがちなトレーダー です。
一方で、長期的な視点(〝期待値〟)で考えるトレーダーは「交換する場合」を選ぶはずです。〝勝率〟は 50%ですが〝期待値〟が高いからです。
この違いが、最終的に 大きな結果の差につながる のです。
「期待値」と「大数の法則」
サイコロの「期待値」や 2つの封筒で紹介した「期待値」は、1~2回、それをやっただけでは再現できません。
例えば、サイコロの「期待値」は約95円でしたが、1回だけなら、5か6の目が出て 150円もらえることもあるし、1の目が出て20円で終わってしまうこともあります。
つまり、「期待値」を再現するには「回数」が必要だということです。
逆に考えるなら、「回数」さえクリアできれば「期待値」は再現できる ということです。
確率pで起こる事象において、試行回数を増やすほど、その事象が実際に起こる確率はpに近づく
引用元�: 統計Web:17-1. 大数の法則1
実験
「大数の法則」がどういうものか、少し実験をしてみたいと思います。
まず、サイコロの目の「期待値」は以下の通り。
| 出る目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| 積 | 1/6 | 2/6 | 3/6 | 4/6 | 5/6 | 6/6 |
サイコロの目の「期待値」
= 1/6 + 2/6 + 3/6 + 4/6 + 5/6 + 6/6 = 21/6 = 3.5
続いて、以下で「サイコロの出た目の平均が『3.5』になるか」を確認する
- サイコロを1,000回振るテストを行う
- サイコロを振るごとに、それまで出た目の平均を記録する
- 同様のテストを100回行う
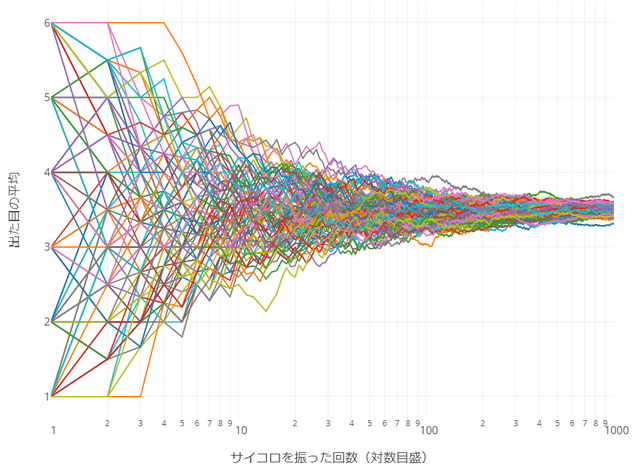
さすがに手でやるのはツライので、Pythonで実験しました。以下がテスト結果のグラフです。
見事に「3.5」に収束しています。
また、試行回数が増える毎に平均に収束 していることが分かります。1,000回目まで行くと、誤差もほとんどありません。
これが「大数の法則」です。
これを投資に応用しようというのが、この記事のテーマです。
times = 1000
tests = 100
result = pd.DataFrame()
for test in range( tests ) :
for time in range( times ) :
result.loc[ time+1 ,test+1 ] = random.randint( 1 ,6 )
result.loc[ time+1 ,f'{test+1}_avg' ] = result[ test+1 ].mean()ギャンブルと「期待値」
まずは、色々なギャンブルの「還元率」をみてみましょう。
| 日本の主な宝くじ | 約45% | スポーツくじ | 約50% |
| 中央・地方競馬 | 約70~80% | オートレース | 約70% |
| 競輪、競艇 | 約75% | パチンコ・パチスロ | 約85~90% |
| カジノ全般 | 約97% |
「還元率」と「期待値」は同じと考えて差し支えありません。つまり、上記のギャンブルをしていると最終的に負けてしまうということを表しています。
宝くじなんて買うもんじゃないですね。当選率も低ければ還元率も低いです。
さて、この記事の冒頭で「プロギャンブラーはビジネスとしてギャンブルをしている」というお話をしました。例えばカジノの還元率(=期待値)は 97%ですが、なぜそんなことができるのでしょうか?
ここには、以下のような違いがあります。
- 「還元率」は、全プレイヤーを含めた「期待値」
- プロギャンブラーの「期待値」は個人(1プレイヤー)の「期待値」
例えば、ポーカーのプレイヤーには、「初めての人」「趣味レベルの人」「下手な人」「プ�ロとしてプレイする人」など、さまざまな人がいます。「還元率」といわれる「期待値」は、これらすべてのプレイヤーをひっくるめたものです。
それに対して、視点を個人に移すと、
- 「プロとしてプレイする人(個人)」の「期待値」は間違いなくプラス
- 「下手な人」の「期待値」はきっとマイナス
であるということです。
投資も同様です。
投資はゼロサムゲームですが、全体で考えるならば、その**「期待値」は「取引手数料」分のマイナスになるはず**です。
しかし、ビジネスとして取引をしている「ファンド」や、投資だけで安定的に生計をたてている「専業投資家」の「期待値」はプラスで、「期待値」を意識していないトレーダーの多くはマイナス なのです。
全体ではなく、あなた自身のトレードの「期待値」が重要 で、その「期待値」は向上させることができます。
投資の「期待値」
あなた自身の「期待値」は、以下の計算式で算出することができます。
使うのは小学校の算数だけです。
ただし、これを算出するためには
- トレードの記録をつける
- あなたの取引会社から売買記録をダウンロードして集計する
等の作業が必要になります。
以下で、「実際のトレードに『期待値』を活かす方法」をいくつかご紹介します。
① 統計 →「期待値」
まずは手法の統計をとってトレードに活かす例です。
- 手法のバックテストをできるだけリアルで十分な量行う
- バックテストの統計データをとる
- 勝率やリスクリワード比率(平均利益と平均損失)から「期待値」がプラスであることを確認する
- バックテスト通りの手法で実際に取引していく
これは、過去の値動きをもとに手法の有効性を測り、プラスであることを確認して実践するというものです。
このブログでもいくつかご紹介していますが、まずは、できるだけリアルなバックテストを行うことが重要です。サンプル数が少ないと結果が偏るので、テストの量も大切です。もちろん、過去の値動きは100%将来を裏付けるものではないため、どんなに結果が良くても盲信してはいけません。
このように注意点はありますが、非常に有効な方法のひとつだと思います。この方法だけで上手くいっている人も少なくないと思います。
② �チャート →「期待値」
エントリー時に目標利益と損失を定めて「期待値」に近づけるというアプローチもあります。例えば次のようなことをします。
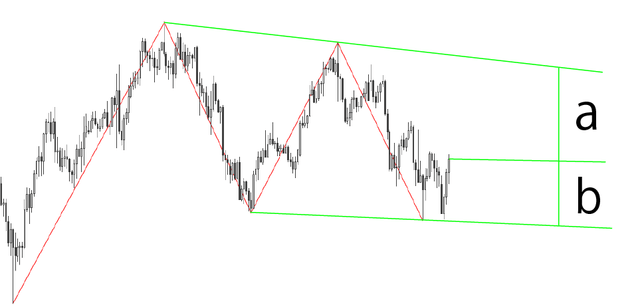
エントリー時に損切りと利益確定を決める
- 図の場合は買いエントリー
- (a) が想定する利益
- (b) は想定する損失
(a) が (b) より大きいときだけ取引し、勝率が50%以上であればトータルで勝てるだろうという試みです。この場合は、あらかじめ得意な形(勝率が 50%以上の形)を探しておく必要があります。
これはレンジ(もみ合い)における考え方ですが、トレンドフォローであっても、トレンドの見込みと想定する損失を比較して取引をすることが重要です。
「見込み利益」を算出
また、「期待値」とその手法のエントリーにおける出現頻度がわかっていれば、「見込み利益」を算出することもできます。
- 期待値が5,000円
- 月に10回程度エントリーすることができる
上記のようなことが分かっている手法ならば、年間の「見込み利益」は以下のようになります。
- 年間の取引回数は「10回 ✕ 12ヶ月」で「120回」
- 年間の「見込み利益」は「5,000円 ✕ 120回」で「600,000円」
もしかしたら、月に10回しかエントリーしないので、損失で終わる月もあるはずです。しかし、120回という取引回数をこなすことができるため、1年が終わる頃には「見込み利益」である「600,000円」に近い数字になっているはずです。
「期待値」が分かっていれば、このように目標を定めることもできるのです。
「期待値」の注意点
最後に、注意点に触れておこうと思います。
再現できなければ意味がない
どんなに良い「期待値」の手法を見つけ出したとしても、それを再現できなければまったく意味がありません。この「再現する」には、いくつかポイントがあります。
- 一定以上の取引回数が必要
- 期待値はゆっくりと再現される
- トレード管理が必須
- 負けが続いても徹底しなければならない
- 連敗に耐えられる資金管理が必要
「1」はサイコロで実験した通りですね。「期待値」が再現されるのには「取引回数」が必要です。「2」も同じ話で「思っている以上に時間がかかるよ」ということです。
そして、ルールを徹底することが必要です。徹底するには「3」のトレード管理が必要で、「4」のように負けが続いたとしても徹底しなくてはいけません。つまり、「5」のように連敗しても破産しない資金の管理(ポジションサイジング)が必要です。
「単利」と「複利」で様変わりする
これまで解説してきた「期待値」は すべて「単利」で運用した場合のもの です。これが 「複利」となると、様変わり してしまいます。
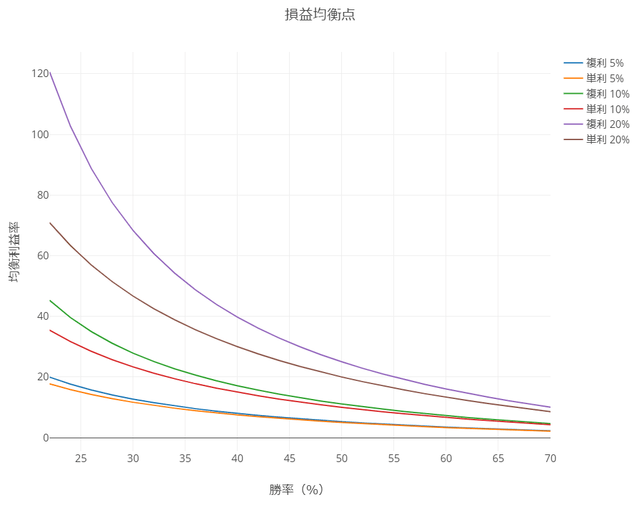
この図は、損益均衡点を表しています。
グラフの読み方は以下の通りです。
| 勝率が50%かつ | (横軸50の目盛り) |
| リスクを10%とる単利運用の場合、 | (緑色のグラフ) |
| 必要な利益率は10% | (縦軸を確認) |
このグラフをもとに、単利と複利の均衡点を比較してみます。
必要な利益率
| 単利 | 複利 | |
|---|---|---|
| 勝率50%・リスク10% | 10% | 11.11% |
| 勝率50%・リスク20% | 20% | 25% |
複利では必要な利益率が増えている ことが分かると思います。
つまり、単利の期待値で複利運用してしまうと、儲かるはずなのになぜか損している ということになります。しかも、「『期待値』の再現には取引回数が必要だ」なんて思っているとどんどん傷口が広がっていってしまうのです。
「期待値」がプラスでも破産する
最後に、「『期待値』がプラスだからって油断しちゃダメだよ」という話をします。「再現できなければ意味がない」の「連敗に耐えられる資金管理が必要」に通じる話です。
この図をみていただくのが、一番分かりやすいと思います。
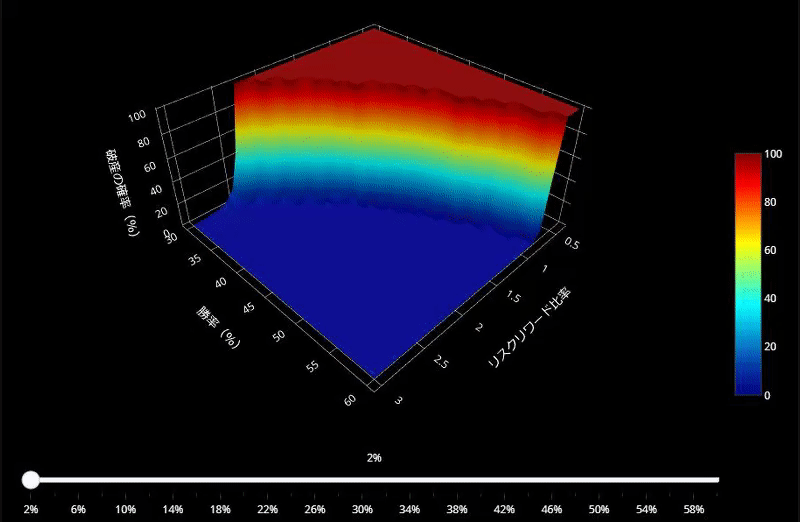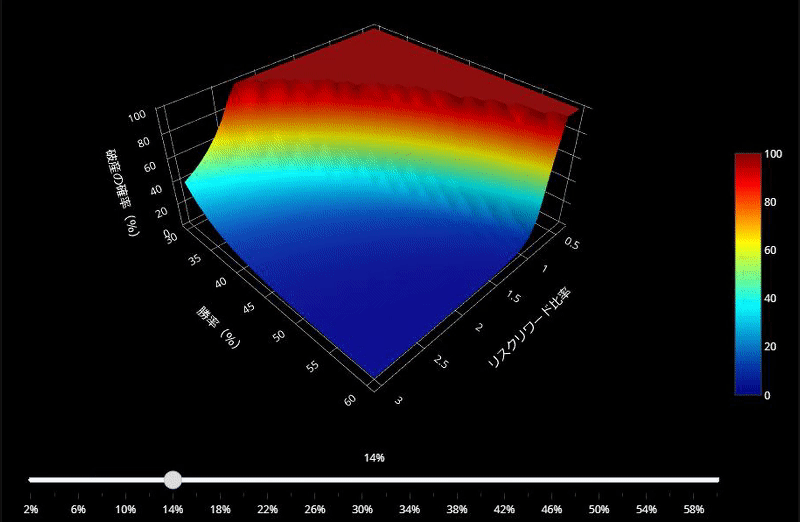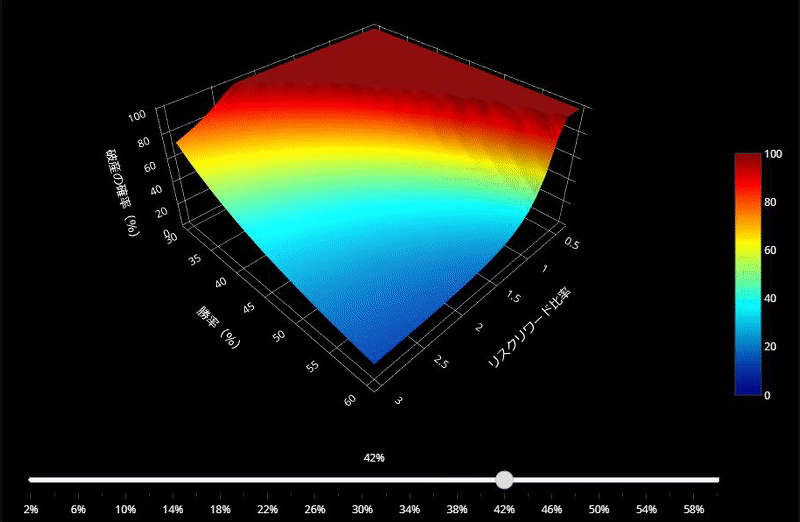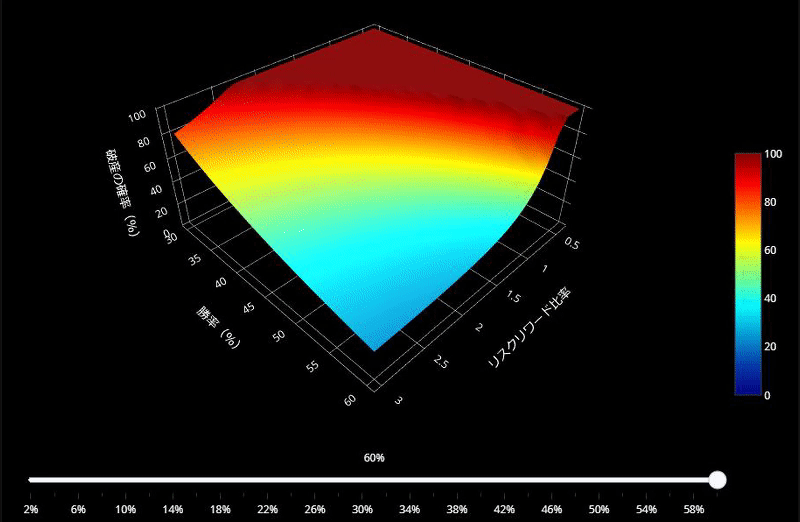
これは「破産の確率」の変化を表したグラフです。
- X軸:勝率、Y軸:平均利益と平均損失の比率、Z軸:破産の確率
- 1トレードでとるリスクを2%~60%で変化させてアニメーションを作成
- 「破産の確率」は1%以下が理想(つまり濃い青のエリアにいないといけない)
このサイトに「『破産の確率』計算機」というものを用意しているので計算してみていただきたいのですが、そもそも 損益分岐点ギリギリ(期待値が±0)のトレードをしていると「破産の確率」は 99% になります。
どんなに1トレードのリスクを抑えても、です。
なぜなら、連敗があるからです。
そして、「期待値」が大きくプラスだとしても、1トレードのリスクを大きく取りすぎてしまうと「破産の確率」が上昇 してしまいます。
あっという間に、いとも簡単に、1%を上回ってしまいます。
すべての投資家は、この事実を認識して、受け止めて、細心の注意を払って取引する必要があります。
〝破産の確率〟計算機 - Investment Tech Hack
〝破産の確率〟の計算ツール。項目と活用している方法の解説もあります。「破産を防ぐ5つのポイント」「破産せずに利益を最大化する3つのポイント」「最短で投資の管理・分析を実現するGoogleシート」など。
investment.abbamboo.com

未来が見えない →「期待値」を積むしかない
投資において、必要なのは統計です。
未来は神様にしか分かりません。
未来が見えない投資��の世界において、やるべきことは「未来の予想」ではありません。
未来が分かるほどの情報はTwitterなんかに転がっているはずもなく、最高レベルの人脈によってもたらされます。正直、追い求めてもあまり意味はないと思います。
未来が見えない投資の世界において、できることは「『期待値』をせっせと積み上げる」ということだけです。しかし、これを続ければ間違いなく良い結果につながります。
資金が少ないときにはリスクをとることも必要ですが、長い目で、せっせと「期待値」を積み上げていくことも必要です。
このブログでは定期的にバックテストを行い、テスト結果と「期待値」を公開しています。また、ボクが勉強してきた知識をまとめたページもあります。ぜひ、ご活用いただき、このブログがあなたの投資の一助になれば幸いです!
長い記事を最後までお読みいただき、ありがとうございましたm(_ _)m
オススメ記事
この記事に興味を持った方には、次の記事も参考に�なるかもしれません。
【1日5分】エクセルで「資金・リスク・期待値」の管理(株、FX、あらゆる投資に)
株の信用取引やFX、仮想通貨の売買における「資金・リスク・期待値」を管理することができます。この記事をきっかけに、資金管理に必要な知識を学んで、必要なツールを手に入れることができます。
trade-tools/how-to-manage-investment


- �記事をシェア