どんな記事
あなたは、「こうしていけば投資で勝てる!」というスキームを持っていますでしょうか。明確なスキームをもってい�る投資家は、意外と少ないと思います。
この記事では、ボクがもっているスキームの根っこの部分をすべて公開しようと思います^^!
裁量取引みたいな経験にもとづいたものではなく統計にもとづいたノウハウです。つまり、「同じように組み立てれば誰でも再現できる方法」です。
この記事に掲載した方法を使うと、ある検証結果があるときに「何回トレードするとどれくらいの利益になるのか」や「そのトレードルールと自分の投資金でどの程度のリスクをとっていいのか」がわかるようになります!
Twitterでも紹介していただいています
ポイント1:トレードエッジ
ひとつ目のポイントは「トレードエッジ」。聞いたこともある方も多いかもしれませんね。ここでは基本的な解説をします。
「トレードエッジはよく知ってるよ」という方はポイント2へ進んでください^^
トレードエッジ = 優位性 = 期待値
エッジ(edge)とは、直訳すると「刃物の刃」を意味する英語ですが、投資においては一般的に「優位性」を指します。
つまりトレードエッジとは、「その投資における優位性」です。そして、統計学や確率論では、その優位性を「期待値」として表すことができます。
トレードエッジ = 優位性 = 期待値
「期待値」とは
Wikipediaで「期待値」について調べると次のようにでてきます。
期待値
確率論において、期待値(きたいち、英: expected value)は、確率変数の実現値を、確率の重みで平均した値である。
例えば、ギャンブルでは、掛け�金に対して戻ってくる「見込み」の金額をあらわしたものである。ただし、期待値ぴったりに掛け金が戻ることを意味するのではなく、各試行で期待値に等しい掛け金が戻るわけではない。
これだけだと、いまいちピンとこないと思います。Wikipediaに掲載されている『くじ引きの「期待値」』を考えてみます。
くじ引きの「期待値」
期待値を理解する上で、次のような計算例がよく取り上げられます。
くじ引きの「期待値」
次のようなゲームを考える。
- 100円支払えば、6面サイコロ1個を1回振ることができる。
- サイコロの目に応じて、次の金額を貰える。
- 20円
- 50円
- 100円
- 100円
- 150円
- 150円
このとき、もらえる金額の期待値を求めると、
期待値 = 20 × 1/6 + 50 × 1/6 + 100 × 1/6 + 100 × 1/6 + 150 × 1/6 + 150 × 1/6 = 95
である。
得られる金額の期待値 95 円が参加費 100 円を下回ることから、このゲームは「参加者が得をする可能性もあるものの平均的には損をする」ということが分かる。特に回数を増やすほど、試行ごとに 5 円の損をした状態に限りなく近づく。
期待値と言うとややこしく感じる人もいるかもしれませんが、すごく簡単ですよね。
それぞれの目に応じたリターンがあって、ひとつの目がでる可能性は6分の1ですから、上記のように計算すればサイコロ1回あたりの期待値がでるわけです。
そして、期待値というのは統計的なリターンの「見込み」ですから、「1回振ると必ずそのリターン」というわけではなく、「長い目でみると、それくらいのリターンになるよね」ということを表しています。
その根拠となるのが、次で解説する「大数の法則」です。
「大数の法則」とは
「大数の法則」は、数学の「統計学」や「確率論」の法則。数学的に証明されている法則 です。投資やギャンブルにおいては、その法則を活用することができます。
大数の法則
数多くの試行を重ねることにより、事象の出現回数が理論上の値に近づく定理のこと
「数学の――」なんて言い方をすると小難しくなりますが、実はすごく当たり前なことを言っています。
上で取り上げたサイコロの例でいうと、サイコロの1の目がでる確率は6分の1ですが、実際には6回振って必ず1回でるわけではありません。2回3回とでることもあれば、まったくでないこともザラにあります。
それに対して、例えばサイコロを6000回振ると、1の目はおおよそ1000回でます。これが「大数の法則」です。
ちょっとした実験で確か�めてみます。
サイコロと「大数の法則」
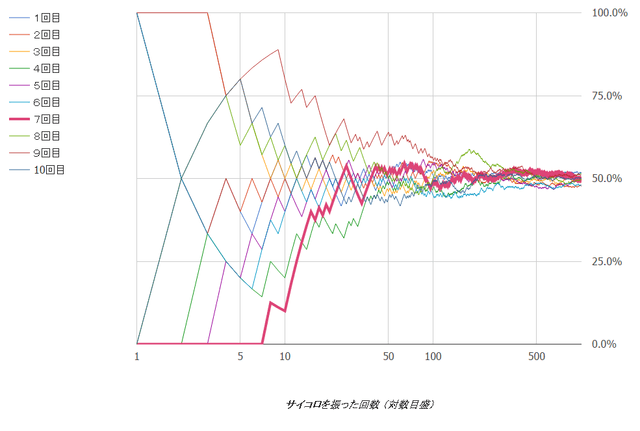
今回は、次のような実験を行ってみました。
- サイコロを振って1~3の目がでた数をカウント
- サイコロを振った回数に対する1~3の目がでた回数の割合を計測
- その推移をグラフにする
- 1000回1セットで10セット計測する
- 理論値は50%
すると、次のような結果になりました。
図を見ると、なんとなく50%に収束していることが分かると思います。サイコロでやってみると非常に分かりやすいですよね。
ここまでで、ポイント1の材料は出揃いました!
次で、ポイント1をまとめます!
期待値は「大数の法則」の終着点
さて、「期待値」は、次のように『「大数の法則」の終着点』を表しています。
『「大数の法則」の終着点』= 期待値 × 取引量 × 取引回数
くじ引きの例で考えてみます。
- 上の例で、サイコロの期待値は95円だった
- この期待値のくじ引きを続けると――
- 『「大数の法則」の終着点』= 95円 × 1 × 600回 = 57000円
くじ引きを1回やるだけでは、当然95円にはなりません。しかし、「600回サイコロを振ると利益は57000円くらいになっているよね」ということを表しています。
では、サイコロの出目が「大数の法則」にもとづいた結果だと、どのようになるのでしょうか。
くじ引きの「期待値」――600回やると?
- 1回のサイコロで100円支払う
- サイコロを600回振ると、次のような結果になる可能性が高い
- 各出目の回数は「大数の法則」にもとづき、ちょうど100回ずつになったと仮定する
- 20円 × 100回 = 2000円
- 50円 × 100回 = 5000円
- 100円 × 100回 = 10000円
- 100円 × 100回 = 10000円
- 150円 × 100回 = 15000円
- 150円 × 100回 = 15000円
- 支払い額 = 100円 × 600回 = 6万円
- 利益 = 2000円 + 5000円 + 10000円 + 10000円 + 15000円 + 15000円 = 57000円
このように、取引回数を重ねれば重ねるほど、勝ったり負けたりしながら「期待値 × 取引量 ×取引回数」の結果に収束していきます。
このサイコロの例は支払い額6万円に対して57000円しか得ていないのでエッジ(優位性)があ��りませんが、「エッジのある手法」をみつけて「期待値」を算出すると、「大数の法則」にもとづいて運用していくことができます。
期待値はバックテストを行うことで導きだすことができます。
つまり、「トレードエッジ」(期待値)はバックテストの結果を実際のトレードに落としこむ有効な手段である と言えます。
ポイント2:破産の確率
2つ目のポイントは「破産の確率」です。これも比較的有名です。トレードエッジに引き続き、ここでは基本的な解説をしますので、「破産の確率は良く知ってるよ」という方はポイント3へお進みください^^
「破産の確率」とは
「破産の確率」を知らない方には、この表をお見せするのがわかりやすいかなと思います。
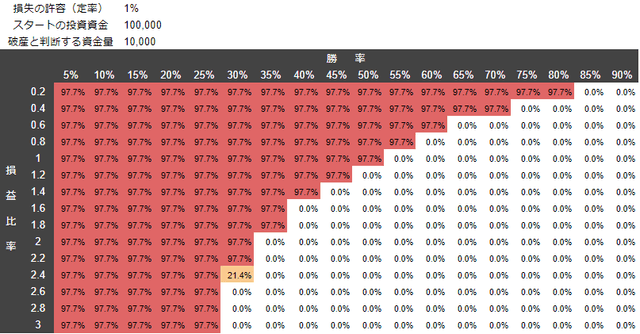
1%のリスクでトレードした場合の破産の確率
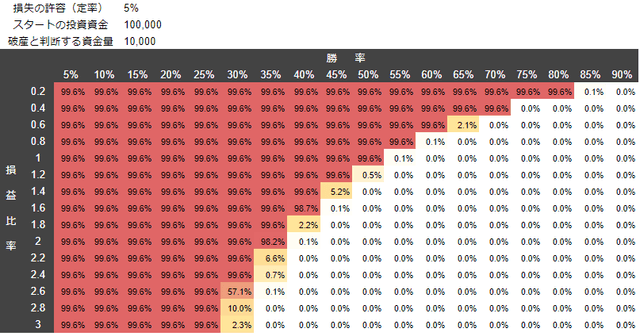
5%のリスクでトレードした場合の破産の確率
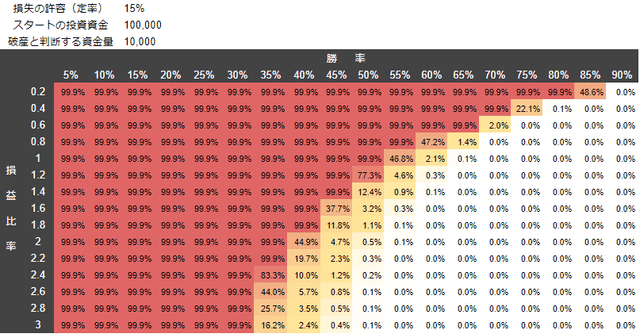
15%のリスクでトレードした場合の破産の確率
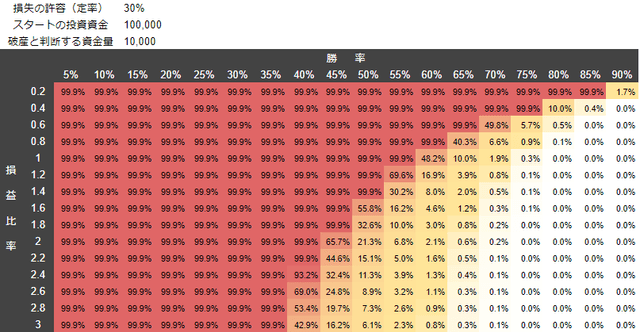
30%のリスクでトレードした場合の破産の確率
60%のリスクでトレードした場合の破産の確率
横軸が勝率、縦軸が損益比率(RR比率)で構成されてる表です。
- 勝率が低い
- 損益比率が低い(利益よりも損失の方が大きくなりやすい)
- 大きいリスクでトレードをする
等で、破産の確率が上昇することが分かります。
破産の確率とは、具体的には次のようなものです。
破産の確率
その投資やギャンブルが破産する確率はどの程度なのかを算出する
以下の3つの項目をもとに算出することができる(実際には5つですが、ここでは割愛します)
- 勝率
- 損益比率(リスクリワード比率、ペイオフレシオ、プロフィットレシオ)
- 損失の許容(掛け金、リスク)
ご存じない方のために、3つの項目の簡単な解説も置いておきます。
勝率
誰もが知っている統計の項目です。勝率50%とすれば、1000回やれば500回くらいは勝てるんじゃないかいというやつです。
損益比率
これは意外と知らない人が多い項目。
そもそも名前がややこしいですね。同じことを意味する言葉がたくさんあります。損益比率とか、リスクリワード比率とか、ペイオフレシオに、プロフィットレシオまで――。
負けるときの平均損失に対して、勝つときの平均利益がどれくらいなのかを表す数値です。リスクリワードが2倍だとすると、負けるときの損失が平均1万円なら勝つときは平均2万円くらいだよねということです。
損失の許容
これはもっと知られていないですね。でも1番重要な項目です。
簡単に言うと掛け金のことです。いくらベットするのか。投資なら、1回のトレードでいくらの損失まで許容するのか。つまり、どれくらいのリスクをとるのかということです。
さて、前置きが長くなってしまいましたが、ここまでわかると表もよくわかります。次でもう1度、じっくり表をみてみようと思います。
重要なのはリスクテイク
見やすいように、同じ表をもう一度のせま�す。
1%のリスクでトレードした場合の破産の確率
5%のリスクでトレードした場合の破産の確率
15%のリスクでトレードした場合の破産の確率
30%のリスクでトレードした場合の破産の確率
60%のリスクでトレードした場合の破産の確率
さて、あらためて見ていくとどうでしょうか。
勝率50%でリスクリワード比率が1倍だと、ほぼ間違いなく破産しますね。
リスクを1%しかとらなくても99%の確率で破産です。つまり、「2回に1回勝つ、勝ち負けはイーブン、リスクは1%」という条件であっても、ほぼ間違いなく破産する んです。ちょっと意外じゃないでしょうか。
次に、青いカーソルのある、勝率50%でリスクリワード比率が2倍の「破産の確率」を見るとどうでしょう。
リスクが数%のうちはどうってことないですが、リスクが上がってくると高確率で破産するという結果になります。 「2回に1回勝つ、勝ちは負けの2倍」という条件であって、そこそこ低リスクでも、高確率で破産するんです。投資って、リスキーですね。
注目するべきなのは、リスクを1%から、2%、3%、15%、30%、60%と増やしていくと、破産の確率もどんどん上がっていく ということです。いくら手法の成績が良くても、リスクを取りすぎてしまうとまったく意味がありません。
ちなみに一般的には、この破産の確率を1%以下に抑えるのが良いみたいです。
「破産の確率」は十人十色
ここまで「破産の確率」について解説してきました。しかし、破産の確率は十人十色です。人によって全然違います。それは次のような感じです。
トレンドフォロー(順張り)の人
ボクもトレンドフォロー派ですが、得てして勝率は低くなりがちです。
勝率が3割とか4割になることがざらにあります。しかし、その分リスクリワード比率をガッツリ高めることができます。例えば3倍とか4倍といった具合です。
逆張り(カウンタートレード)の人
逆張りは、高い勝率になる傾向があります。日本人は逆張りのトレーダーがすごく多いですね。
逆張りの勝率は6割とか7割ですね。その分、大きくやられやすい傾向があります。そして、大きくとれません。そうするとリスクリワード比率は1倍以下になってしまうことが多いです。典型的なコツコツドカンタイプですね。
番外編:定まっていない人
ここであえて書かせてください。定まっていない��人は大変危険です。
割り切って授業料だと思ってやっているのなら良いですが、そうでないなら一旦勉強をするべきだと思います。他にも、いろんな手法がごちゃ混ぜでひとまとめに運用しているとか、よくわからないままに取引量を決めていたりとか、トレードの記録をつけていないとか――。本当に危険です。ご注意ください。
手法はなんでも良いんです。
トレンドフォローでも逆張りでも、短期でも長期でも、テクニカル分析でもファンダメンタルズ分析でも、正直なんでも良いんです。一定水準以上のエッジがあるなら、あとは自分にあった手法が一番です。
大事なことは、自分の手法をしっかり把握すること です。
勝率はどうなのか、リスクリワード比率はどうなのか。そして、破産の確率を1%以下におさえるためには、どれくらいのリスクテイクが適正なのか。その手法で、破産しないギリギリのリスクはどの程度なのか。そんなことが重要です。
ポイント3:トレードに活かす
さてさて、ここからは「エッジと破産の確率を活用する方法」を具体的に解説していこうと思います。
モデルケース:Aさん
ここでは、モデルケースとしてAさんに登場してもらいます。Aさんがバックテストで発見した手法を、いかにして実践に落とし込むのか。
Aさんの手法の検証結果は次の通りであったと仮定します。
ある手法の検証結果
- 勝率:50%
- 平均利益:2万円
- 平均損失:1万円
この手法の期待値を算出すると次のようになります。
期待値を計算する
期待値 = 20,000円 × 1/2 − 10,000円 × 1/2 = 5,000円
一回のトレードの見込み利益は5,000円となりました。
Aさんの統計的な終着点
この手法において、「大数の法則」の終着点は、次のように考えることができます。
「大数の法則」の終着点
5,000円 × 1倍(取引量)× 100回 = 50万円
取引量というのは、FXなら10000通貨とか、株なら1000株とか、そういう話です。今回、ここでは1倍としています。つまり、検証時と同量での運用としています。
この手法がどんなエントリーのサインか明らかになっていませんが、そのサインにもとづいて100回トレー��ドをする頃には50万円くらいの利益があがっているだろう ということです。
どうでしょうか。
回数を重ねるほど『「大数の法則」の終着点』の金額に近づいていくのは、「サイコロと『大数の法則』」で紹介したグラフをみていただくと何となくイメージがわくと思います。
そして、投資ですから資金が許せば取引量はいくらでも増やせますよね。
例えば、取引量を100倍とすると次のようになります。
5,000円 × 100倍(取引量)× 100回 = 5000万円
一定のサインですから、意図的に取引回数を増やすのは少しむずかしいかもしれませんが、
例えば、時間軸を短くして日足から4時間足にしてみたり、取引銘柄を1銘柄から10銘柄に増やしてみたり、そんな取引回数を増やすアプローチもあります。
工夫をこらして取引回数も増やすとどうでしょうか。
5,000円 × 100倍(取引量)× 1000回 = 5億円
取引量を100倍にして、この手法のサインで1000回取引すると、それだけで5億円です。夢がひろがりますよね!
リスクのとり方が結果を大きく左右する
さて、取引量が100倍で1000回の取引回数とすると、ひとつ問題があります。それは、「投資金がどの程度あるのか」です。
どうして問題なのでしょうか。
投資金100万円でのトレードでイメージしてみるとわかりやすいと思います。
- 投資金: 100万円
- 「大数の法則」の終着点: 5,000円(期待値)× 100倍(取引量)× 1000回 = 5億円
- 平均利益と平均損失も100倍になる
- 平均利益: 20,000円× 100倍(取引量)= 200万円
- 平均損失: 10,000円× 100倍(取引量)= 100万円
はたして、このトレードで破産せずに生き残っていくことはできるでしょうか。
正直、むずかしいですよね。
問題は、トレードの平均損失 です。
もちろん「平均損失」ですから、毎回��この金額になるわけではないです。しかし、投資金が100万円しかないトレーダーが、平均損失100万円の取引をするとどうなるか。
破産の確率を計算するまでもなく、破産してしまうことが容易に想像できます。
目指すべきは「破産の確率」1%未満
では、どの程度のリスクが「適正」なのか。
投資をするうえで、 破産するかしないかのギリギリのラインがわかるとしたら、そのラインより少ないリスクで投資をすることはせっかくの利益を放棄していると言えます。過剰に警戒してリスクをおさえてしまうと利益も少なくなってしまいます。それはもったいないですよね。
そのラインがわかっているのなら、最大限までリスクをとって利益を最大化するべき だとボクは考えています。ここで言う「適正」は、そういう意味での「適正」です。
そこで登場するのが「破産の確率」です。
「破産の確率」に必要な項目は「勝率、リスクリワード比率、損失の許容(リスク)」でした。
- Aさんの検証結果
- 勝率:50%
- 平均利益:2万円
- 平均損失:1万円
- リスクリワード比率:2倍
- 「破産の確率」に必要な項目を当てはめる
- 勝率:50%
- リスクリワード比:2倍
- 損失の許容(リスク):破産しないギリギリのリスクが知りたい
- 破産の確率:1%以下にする
繰り返しますが、破産の確率は1%以下におさえます。
つまり、知りたい「損失の許容(リスク)」以外の項目はすべてわかっています。
ここまできたら簡単です。
破産の確率を求めるツールがありますので、そのツールで計算するだけです。
以下は、ざっくりと計算してみた結果です。
- 投資金:100万円
- 取引量:100倍
- 平均損失:100万円(1万円 × 100倍)
- 損失の許容(リスク):100%(平均損失 / 投資金)
- 破産の確率:100%
- 取引量:50倍
- 平均損失:50万円
- 損失の許容:50%
- 破産の確率:99.93%
- 取引量:30倍
- 平均損失:30万円
- 損失の許容:30%
- 破産の確率:4.53%
- 取引量:20倍
- 平均損失:20万円
- 損失の許容:20%
- 破産の確率:0.11%
どうでしょうか。
こうやって順を追って考えていくと、100倍の取引なんてとんでもなくて、せいぜい20倍強の取引量でなければいけないことがわかりますよね。
注意したい点は、「この取引量よりもいちじるしく少ないリスクも良くない」ということです。
この手法と投資金(元金)においては、20倍が適正な量です。
Aさんのとるべき戦略は
ここまでくると、大数の法則の終着点で残る項目は取引回数だけです。
「大数の法則」の終着点 ――Aさんの手法の場合
5,000円 × 20倍(取引量)× 取引量
ひとつの手法があって投資金(元金)がはっきりしていると、ここまで明確にすることができます。あとは、「いかに取引回数をこなしていくか」ということだけが問題になってきます。
例えば、日足の1銘柄で年間100回くらいしかサインがでない手法だとすると、時間軸を短くしたり、銘柄数を増やすことで取引回数を増やすことができます。
- 5,000円 × 20倍(取引量)× 100回 = 1000万円
- 5,000円 × 20倍(取引量)× 1000回 = 1億円
取引回数を1000回まで増やすこ�とができたとすると、1億円を目指せるということがわかります。
4.まとめ:攻めのリスク管理とは
ここまで解説してきたスキームは、誰でも活用することができます。
必要なのは、「あなたの手法の勝率とリスクリワード比率、そして投資金(元金)がいくらあるのか」だけです。
むずかしいことはひとつもないと思います^^
せっかく良いトレードエッジが見つかっても、こわがってリスクを極端に避けてしまうと利益が減ってしまいます。しかし果敢にリスクをとりすぎてしまうと破産してしまう。
これらを両立する「最もちょうどいいリスク」を算出することでトレードエッジを最大限活かすことができます。破産せずに利益を最大化できるリスクの量 にすることが重要です�。
ぜひ、あなたのトレードにも取り入れることをオススメします^^!

- 記事をシェア