どんな記事?
同じ「期待値」と「取引回数」であっても、勝率重視の手法なのか、RR比重視なのかの違いによって大きな違いがあります。この記事を読むことで、�次のことが分かります。
- 勝率重視とRR比重視どちらが有利なのか
- 複利運用をする上でどんな点に注意するべきなのか
今回の記事を書くにあたって、アンケートをとってみました。
最も多かったのは「RR比重視が有利」の回答。実は私自身も同じ考えでした。
果たして、どちらが有利なのか。 シミュレーションをしてみると、驚くほど顕著な違いがありました。
勝率重視とRR重視とは
すべての手法には期待値というものがあります。「その手法が勝てる手法なのかどうか」を測ることが��できる数値で、勝率とRR比から算出することができます。
計算式は以下の通りです。
1トレードあたりの期待値
この式から算出される期待値がプラスであるなら、それは勝てる手法であるということを表しています。もちろん、勝率やRR比とい��った統計が信頼に足るものである必要があります。そして、必ずというわけでもありません。
今回は細かい条件の話をしたいわけではないので、詳細が知りたい方は以下の記事を読んでみてください。自分で言うのもなんですが、けっこう詳しく書いてあると思います。
で、その期待値を算出したのが以下の表です。
| 勝率 | 80% | 70% | 60% | 50% | 40% | 30% |
|---|---|---|---|---|---|---|
| RR比 | ||||||
| 0.5 | 0.2 | 0.05 | -0.1 | -0.25 | -0.4 | -0.55 |
| 1.0 | 0.6 | 0.4 | 0.2 | 0 | -0.2 | -0.4 |
| 1.5 | 1.0 | 0.75 | 0.5 | 0.25 | 0 | -0.25 |
| 2.0 | 1.5 | 1.1 | 0.8 | 0.5 | 0.2 | -0.1 |
| 2.5 | 1.8 | 1.45 | 1.1 | 0.75 | 0.4 | 0.05 |
| 3.0 | 2.2 | 1.8 | 1.4 | 1.0 | 0.6 | 0.2 |
この表で、今回、注目してもらいたいのは次の2箇所です。
- 勝率:80%、RR比:0.5 → 期待値:0.2
- 勝率:30%、RR比:3.0 → 期待値:0.2
どちらも期待値は同じ0.2ですが、「1」は勝率が高くRR比が低い、「2」はRR比が高く勝率が低いことが分かります。これが表題の「勝率重視」と「RR比重視」です。
で、このことについて色々と気にしなければならないことはあるのですが、今回とくに注目したいのが「複利運用においても同じ結果なるのかどうか」ということです。
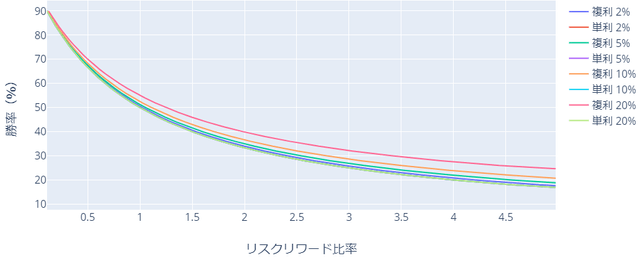
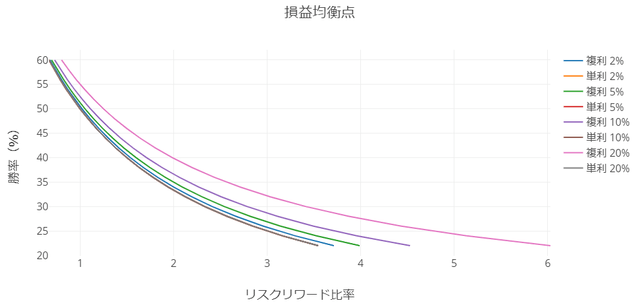
単利と複利の違いは、このグラフが最も分かりやすいと思います。
このグラフは、損益分岐点、つまり期待値がゼロのポイントを表したものです。単利と複利で違いが生じていることがわかると思います。リスクのとり方で単利と複利の運用結果は大きく変わります。そして注意しなければならない点は「前述の表はあくまでも単利運用での期待値である」ということです。
この記事では、単純化したシミュレーションを行い、複利運用における勝率重視とRR比重視の違いを紐解いていきたいと思います。
シミュレーションの条件
シミュレーションはPythonで以下のコードを用いて行いました。
def test_fixed_rate( win_pct ,risk_reward ,risk_rate ,start_asset ,ruin_line ,times ) :
raw = pd.DataFrame()
for time in range( times ) :
is_win = np.random.rand() <= win_pct
risk_source = start_asset if time==0 else raw.loc[ time ,'balance' ]
risk_value = risk_source * risk_rate
profit_loss = risk_value * np.random.normal( risk_reward ,risk_reward ) if is_win else risk_value * -1
balance = start_asset + profit_loss if time==0 else raw.loc[ time ,'balance' ] + profit_loss
raw.loc[ time+1 ,'result' ] = 'win' if is_win else 'lose'
raw.loc[ time+1 ,'is_win' ] = 1 if is_win else 0
raw.loc[ time+1 ,'risk_value' ] = int( risk_value )
raw.loc[ time+1 ,'profit_loss' ] = int( profit_loss )
raw.loc[ time+1 ,'balance' ] = int( balance )
if balance < ruin_line : break
return raw- 勝ち負けは設定の勝率になる範囲でランダム
- 損益も設定のRR比になる範囲内でランダム
- 毎回のトレードでとるリスクは設定値で固定
ザックリ解説するとこんな感じです。このシミュレーターを以下のコードで実行しました。
start_asset = 1000000
ruin_line = 100000
win_pct = 0.8
risk_reward = 0.5
risk_rate = 0.02
times = 1000
tests = 100
if __name__=='__main__' :
list_result = []
for test in range( tests ) :
raw = test_fixed_rate( win_pct ,risk_reward ,risk_rate ,start_asset ,ruin_line ,times )
list_result.append( raw )1000回売買するテストを100セット、元金は100万円。勝率、RR比、1トレードのリスクは適宜変更してシミュレーションしています。
複利運用のシミュレーション
今回のテストでは「勝率重視とRR比重視のどちらが有利か」を測るために、大きく前述の2パターンのシミュレーションを行いました。どちらも同じ期待値になる組み合わせです。
- 勝率:80%、RR比:0.5 → 期待値:0.2
- 勝率:30%、RR比:3.0 → 期待値:0.2
そして、複利はとるリスクによって成果が大きく異るため、以下の2パターンのリスクを組み合わせて、全4パターンの検証を行っています。
- 一般的なリスク2%の運用
- 現実的な高めのリスクとして10%の運用
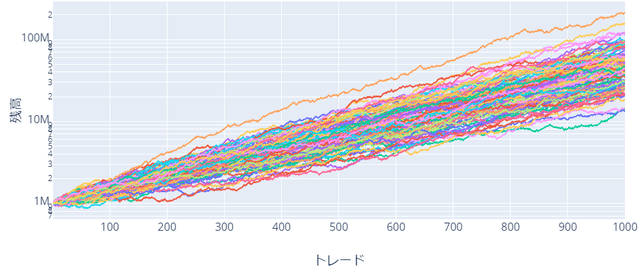
勝率:80%、RR比:0.5、リスク:2%
まずはリスク2%の勝率重視。
勝率:30%、RR比:3.0、リスク:2%
次にRR比重視です。
意外なことに、大きく印象のことなるグラフが出来上がりました。リスク2%でここまで大きな差がでることは想定していなかったので非常に驚きました。具体的には以下のような特徴が見られます。
- 勝率重視の方が安定している(RR比重視と比較してばらつきが少ない)
- RR比重視は「破産」が発生している
- 最高損益はRR比重視の方が圧倒的に良い(200Mに対して1B → 5倍)
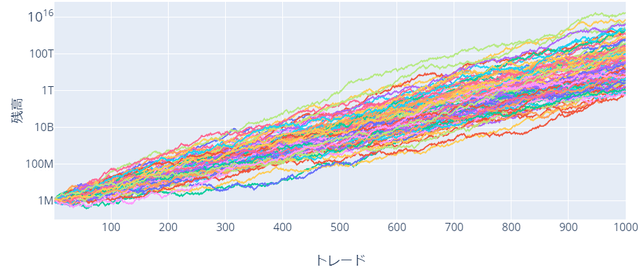
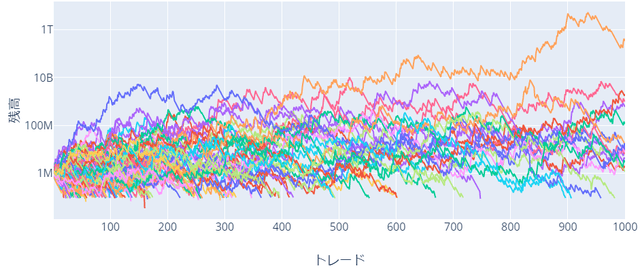
勝率:80%、RR比:0.5、リスク:10%
次に、リスク10%にして同様のシミュレーションを行いました。
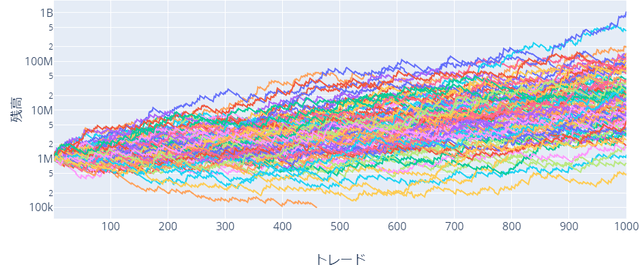
勝率:30%、RR比:3.0、リスク:10%
結果は一目瞭然ですね。勝率重視は、ばらつきがあまり増えないままに収益が改善。RR比重視は、壊滅状態です。100セットの半分以上が破産になっているように見えます。勝率重視については、まだ余裕すら感じます。
結論
複利運用において、勝率重視の方が圧倒的に有利
これが、今回の検証を経た私の結論です。圧倒的に有利だと思います。リスク2%でも差がでるし、勝率重視の方がリスクを大きく取れます(破産強度が高い)。当然、その分収益力が上がります。今後の手法探しは、間違いなく勝率重視で行なうと思います。「本当に良いことを知ったな~!」と思っています。
他にも検証をしながら感じたことがありましたので、以下にまとめます。
大数の法則を実現するための取引回数が異なる
今回の結果を別の切り口で考えてみると、こういうことなんじゃないかなと思います。同じ期待値であっても勝率が高い方が安定する。つまり、「早々に期待値が実現できている」とも考えることができると思います。言い換えるなら、RR比重視の手法は1000回ではなく、1万回くらいのシミュレーションにすれば安定したグラフに見えるんじゃないかなと思います。試していませんが。
「トレンドフォローのストラテジーは分散投資が大事だよね」というのも、このあたりが関係していそうな気もします。取引回数が必要だということですね。
勝率重視の方が破産強度が高い
今回の4パターンの破産の確率を算出してみました。
| 勝率 | RR比 | リスク | 破産の確率 |
|---|---|---|---|
| 80% | 0.5 | 2% | 0% |
| 30% | 3.0 | 2% | 0% |
| 80% | 0.5 | 10% | 0% |
| 30% | 3.0 | 10% | 44.07% |
明らかに勝率重視の方が破産強度が高いことが分かります。「30%、3.0、2%」のパターンについては「破産の確率」が0%なのに「破産」が1回発生していたことにも注意が必要そうです。
ロットの決定時にこのシミュレーションをした方が良い
以前から考えていたことですが、「破産の確率」とか「期待値」ではすべてを測ることはできません。有効ですし、必要ですが、あくまでもひとつの指標でしかありません。
銘柄や足種を変えれば勝率やRR比が変わるので、シミュレーションをしてみないと今回の「損益曲線のばらつき」にはたどり着けなかったと思います。今まで手法の決定には「期待値」(など)、リスクの決定には「破産の確率」を用いていましたが、今後はこのシミュレーションも加えていこうと思います。
実はリスク2%の結果は、単利の結果と大差ない
すこし拡大して再登場ですが、このグラフで単利は一番左下の線です。で、複利になると、取るリスクが増えるごとに右上に移動していきます。つまり、プラスマイナスゼロにするために必要な勝率だったりRR比の要件が厳しくなるんですね。これが単利と複利の違いです。
ここでもう一度、今回のシミュレーションの結論ですが、
複利運用において、勝率重視の方が圧倒的に有利
これ、たぶん単利運用であっても同じことが言えます。単利運用であっても、勝率が高いほど期待値の再現が早いです。RR比重視だと、損益曲線のばらつきが大きくなりやすいです。
複利運用においては、単利運用における期待値が同じでも、RR比重視やリスクの増大に応じて期待値の低下や破産の確率の上昇がみられる
まとめると、こんな感じなんじゃないかなと思います。
補足:RR比重視が悪いわけではない
誤解を避けるために補足しておきますが、RR比重視が悪いというわけではありません。例えば、裁量取引の兼業トレーダーはRR比重視の手法が良いだろうなと思います。
今回の結論は、あくまでも数字上の話です。「同じ期待値」「同じ取引回数なら」という話です。ここには、トレードスタイルやライフスタイルが考慮されていません。圧倒的な期待値が得られるなら、当然、RR比重視で良いと思いますし、同じ期待値であっても「様々な要因を考慮した結果、RR比重視が良い」という結論も十分にあり得ると考えています。

- 記事をシェア