03. 〝目標利益〟から〝複利の利率と期間〟を逆算する

どんな記事

株式投資やFXで100万円を10年で2000万円にすることを目標としたときに、1年の平均利率がどれくらいあれば達成できるのか――。これを年平均成長率といいますが、この計算、単純なようで式を知らないと計算できません。今回は、この計算方法を解説します。すでに知ってる方はスルーしてください笑

複利とは

一言に「毎年○○%の利益で運用していく――」といっても、単利と複利の2通りあります。まず、単利は元金が固定です。例えば、100万円を単利・年5%で運用すると、何年たっても毎年5万円の利益です。それに対して、複利・年5%で運用したときの年利は、1年目が5万円、2年目5.25万円、3年目5.51万円と増えていき、10年目には7.75%になるんです。なぜかというと、前年の利益を含めた金額を元金として運用していくから。その効果は利率が大きくなればなるほど、指数関数的に大きくなっていきます。複利はとんでもない力を秘めているんです。

2．72の法則

これは、今回、複利について調べていて初めて知ったんですが、「へえ〜！」と思ったので、皆さまにもご紹介を。

72の法則は、複利のとき、預けた（または借りた）金額が何年（または何か月）で元の2倍になるかを概算する方法であり、72を利率（％）で割った値がほぼ正しい期数になる。また逆に、72を期数で割った値がほぼ正しくその期数で2倍になる利率になる。

出典 Wikipedia「複利」

つまり、「資金がある利率で2倍になるのに何年かかるか」を求めるのなら、この法則で簡単に計算できますよー、という法則です。これはなかなか便利。

どちらも、確認のために計算してみましたが、まさしくでした。「72」というのは不思議な数字ですね。

CAGR（年平均成長率）

さて、前置きが長くなりました。一番みなさんにお伝えしたかったのはこれなんです。CAGRとかいってしまうと、なにやら小難しい雰囲気を感じるかなと思いますが、実のところ、まったく難しくありません。

CAGRとは

Wikipediaで調べてみると次のように記載されています。

年平均成長率（ねんへいきんせいちょうりつ、Compound annual growth rate, CAGR）とは、指定した期間に亘る成長率から、1年あたりの成長率として算出した幾何平均のことである。

出典 Wikipedia「年平均成長率」

CAGRとか成長率とか、幾何平均とか、、ややこしいですね・・・。
かいつまんでいうと、

「ある資金をある金額まで増やすのに、何%の複利で運用していくと達成できるの？」

ということがわかるようになります。あとは公式に当てはめればいい。テストにでるわけでもないので、それでいいんです。

CAGRを計算する

公式は次のとおりです。

これをもとに、何か例題を解いてみましょうか。

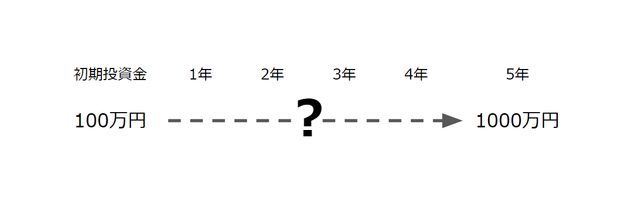
何でもいいのですが、、例えば、100万円の資金を5年で10倍に、つまり1000万円にするには、年利何%で運用できればいいのかを計算してみるとします。
公式に当てはめると次のようになります。

毎年、58.5%ずつ資産を増やしていけば5年で1000万円になるということですね。結構大変。

複利で失敗しないために

複利で運用していくうえで、注意点が2つあります。

これ、ホントに大事です。これらを守る守らないで、億り人と破産者くらいの違いがでてきます。詐欺にあったりもするかもしれないですね。

いや、決して大げさではないです。ホントに。理由がわからない方、知りたい方は、「複利の罠」をお読みください。ぜひ。